在5月12日，钟南山院士的团队在医学杂志JAMA-Medical发表了研究成果“Development and Validation of a Clinical Risk Score to Predict theOccurrence of Critical Illness in Hospitalized Patients With COVID-19”。我翻译成中文是“COVID-19的住院病患产生重症的临床风险评分预测方法的开发和验证”。

看到新闻后的时间我就登陆了JAMA对论文进行阅读，费了一些劲儿才把文章看完。说实话这辈子如果不是因为拜读钟院士团队的文章，恐怕到老都不会接触那些医学专业术语，像是neutrophilia（中性白细胞增多）、coagulopathy（凝血病）……通篇阅读完之后我有以下几点感触和启发，这些想法也增进了我对数据分析认识上的深度解读。下面我就来简单说下我的这几点感受。
 
同一场疫情下，不同模型所产生的认知差异
今年年初COVID-19疫情汹涌而来，而且又还是一个新的未知病毒作祟，人们都很紧张。普通老百姓担心的是疫情的病毒的传染能力、如何避免传染、是否高致死等关系切身生命安全的问题。

大家回忆一下疫情初期朋友圈里热衷于探讨“繁殖率R0”的文章里面，民间有一些机构和学者研究计算的值也各不相同。有人说是2.4，也有人说是4.5……。然而很多人只记住了“一个人传几个人的繁殖速度”，却没有看到这个指标背后的很多基础假设和计算背景。不过这也不怪大家，因为我们都是非医学专业的。这些各种版本的R0在民众惊恐心理支配下，被很多不良的自媒体拿来各种歪曲炒作。我在认真学习了经典的传染病模型知识之后，看了很多搞文艺，或者号称研究区块链的自媒体也在发表文章，通过对R0来预测疫情了！看着半桶水哐当哐当地论调在博眼球，还没读完我就很想笑，到后来就干脆不想看了。老百姓对模型的研究理解，大致就是到这个层面。

钟南山院士团队篇关于预测感染人数的论文，是应用了改良后的经典传染病模型SEIR。刚好我在这次疫情期间也对这个模型进行了研究，通过对模型的研习，我发现定量的分析能够以一个更高的视角看问题。

比方说深度理解疫情下那么多防控措施背后的为什么，进一步看懂社会医疗资源为什么进行这样或那样的分配……等等。这里有一个基本的逻辑关系，就是确诊人数的增长速度和模型的预测进行比对，可以用于校验前期模型的合理性。如果确诊人数增长过快，那么说明原先模型的假设以及参数已经失效，相对应的原有防控措施需要更加严格。而如果确诊人数增长符合模型预测，或者趋缓，甚至下降，那么就说明原有的防控措施是有效的。

以经典的传染病模型SEIR为例，里面有2个重要参数：感染者有效接触易感染人群的速率λ、感染率β。而大家在整个疫情期间所经历过的各种封闭管制，其实都是在控制不让这2个参数继续变大。

例如大家熟知的停止举办大型群聚活动、春节假期延长、公共交通停运、小区封闭式管理、戴口罩出门……只要不主动的聚集，控制好人员的流动，那么感染速率λ和感染率β就能控制住或者降低。当然随着疫情的发展，管制措施的逐步调整，对这两个参数的估算也是不断地动态变化的。

另外单独说一下模型中的这个参数：感染者有效接触易感染人群的速率λ。这次疫情中，包括国外抄作业都抄错的意大利等西欧，都发现单纯的封闭禁足是难以控制疫情的发展。因为家族传播在疫情扩散中扮演着非常重要的角色。要知道一家人中只要有一个被传染了，那么在居家禁足令的实施下，整个封闭的家庭是很容易全部“中招”的。这个时候λ在一个家族传播路径中就会变得很大，按照人的居家特点，λ=5或者=8都是正常不过。这样一来，也就难怪感染人数的发展非常快。另外这次疫情发现家族传播的病征都是普遍轻度或中度为主，如果这个时候能够识别和进行隔离，那么将会有力的阻断病毒的传播和感染者病情的发展。

面对家族传播的这一特点，知道了一个家庭某个人确诊，就可以预算出全家人所需要的病床资源，举一反三进行测算，更可以估计出某个区域未来潜在的病床需求数量。可问题是医院的病床远远不够，怎么办？这个时候一些大型的公共设施，例如体育馆、学生宿舍……被划拨出来建设成“方舱医院”。由于方舱医院改建难度低，模块化的组合也可以根据家族传播路径成片区的安置病人。事实证明，方舱医院的投入使用极大的缓解了病床资源的紧张局面，及时的治疗有效的降低了轻症病患向重症患者的发展，同时也有效隔离了感染者更多的接触易感染人群。这样一来，家族传播在疫情中解释了λ的结构变化；而方舱医院的投入，单从控制家族与家族间传染的视角来看，反过来有力的控制住了λ。

以上是从一个较为宏观和定量的视角来感知模型（通过预测感染人数来整合社会医疗资源）。
 
钟南山院士团队这次在JAMA-Medical杂志上发表的论文，则是从一个微观和定量视角来应用模型。

简单的对这个模型的应用做下介绍：
模型和工具开发的目的，是为了尽早地识别和预测COVID-19感染者演变成重症的可能性，因为它有助于提早准备治疗资源和安排适当的治疗措施。

为了能更好的说明这个问题，我引用了一下百度百科对ICU病房的介绍。因为ICU是重症新冠患者治疗的重要医疗资源。重症患者一般都是需要ICU即重症加强护理病房（IntensiveCare Unit）来开展治疗的，ICU因此也叫作加强监护病房综合治疗室。在ICU里面治疗、护理、康复均可同步进行，为重症或昏迷患者提供隔离场所和设备，提供护理、综合治疗、医养结合，术后早期康复、关节护理运动治疗等服务。

本次的疫情在武汉的一些重症患者还要进入到“火神山”、“雷神山”治疗。在ICU里面，每床位的占地面积为15-18㎡，床位间用玻璃或布帘相隔。ICU的设备必须配有床边监护仪、中心监护仪、多功能呼吸治疗机、麻醉机、心电图机、除颤仪、起搏器、输液泵、微量注射器、处于备用状态的吸氧装置、气管插管及气管切开等所需急救医疗设备。在条件较好的医院，还配有血气分析仪、微型电子计算机、脑电图机、B超机、床旁X线机、血液透析机、动脉内气囊反搏器、血尿常规分析仪、血液生化分析仪等。以上的医疗设备资源的高度利用，充分说明了普通病房和ICU病房的在硬件上的区别。而一家医院或者一个地区的有ICU病房的医院数量是有限的，如果大家都害怕自己万一感染确诊后会发展成重症，都往有条件的医院挤，那样不仅容易造成医疗资源的挤兑，也会造成医疗资源的不合理分配。可如果说一开始确诊时没有识别出短期内会发展成重症的“高风险”病患，把他放在普通病房接受一般的治疗，则容易错失治疗的时机，原本有机会康复的病患却因此造成了悲剧。所以，一旦新冠病患能够在确诊的同时，能预测出短期内是否会发展成重症就尤为重要了。

可问题摆在这里，一个新冠患者的检测指标多达72项，哪些指标能对这个“潜在风险”起到关键指示作用？ 如果能把它们提炼出来是非常有价值的。因为并不是所有的医院都能检查这么全面，也并不是所有的医院的医生都参加了这次疫情的“湖北会战”，有和新冠病毒的实战经验。拿到检测结果却难以做结论的医生肯定不在少数。另外，这些关键指标的数值要严重到什么程度，才容易判定或者识别成高风险患者，这就需要有一套模型来测算。如果模型搞的很复杂，要求医生除了有专业知识和丰富的临床经验外，又还要懂大数据的数学模型算法，那实在又太强人所难。因此，模型工具的简单化和亲民化是第二个现实的问题。 所以，这次钟南山院士团队所开发的工具，解决的就是以上两个比较微观的定量难题。

我看了一下钟院士团队的终成果，挺方便实用的。就是在下面的地址中，http://118.126.104.170/  输入10个关键的检测指标，然后点击测算就可以了。我尝试填写了一下，结果显示我属于“低危人群”

模型选择上的原则——可解释优先
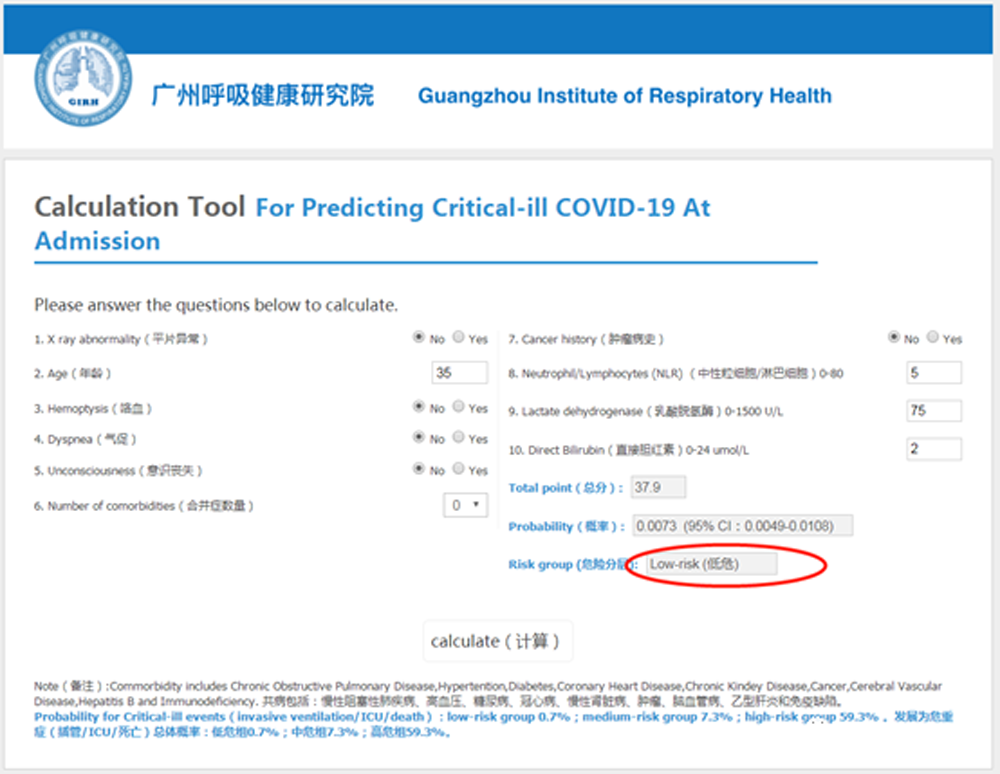
曾经大数据很火的2016年，业界对各种神经网络的算法尤其热捧。大家写论文也好，出方案也好，如果没有用上神经网络或者深度学习，好像就是落伍了一样。当然，我也没有免俗，人非圣贤嘛！毕竟神经网络算法的优点摆在那里，就是在分类算法中识别率很高！但是神经网络或者深度学习有个很大的问题一直无法彻底解决，那就是很难解释参数和超参数。也就是说这些参数或者超参数的现实意义是什么（物理解释）讲不明白。比方说网络结构中为什么隐藏层是5不是4，如果是5能代表什么现实意义？学习率为啥要设定为0.01不是0.015?总之很多地方谁都不能说得明白，所以这类算法也成为“黑盒子”。

 与“黑盒子”难以解释相对应的是可解释的算法——统计模型

统计模型中经典的则以各种线性模型以及可做线性变换的曲线模型为代表。不过线性模型有个的问题，就是拟合偏差比较大。而且我还是在学生时代，就发现很多经典的线性模型偏差太大！说到底因为现实的场景往往不是线性的结构。还有很多大数据相关的教材、讲课视频，入门的算法都是线性回归；当介绍完线性回归之后，立马就跳入了比较复杂的算法中去了。例如神经网络中计算梯度下降的公式中，会涉及到线性方程的计算部分。因此讲线性回归是为了引出“梯度下降”。不过这些跳跃经常让人难以适应。但线性模型的优点就是可解释性非常强。举个例子来说

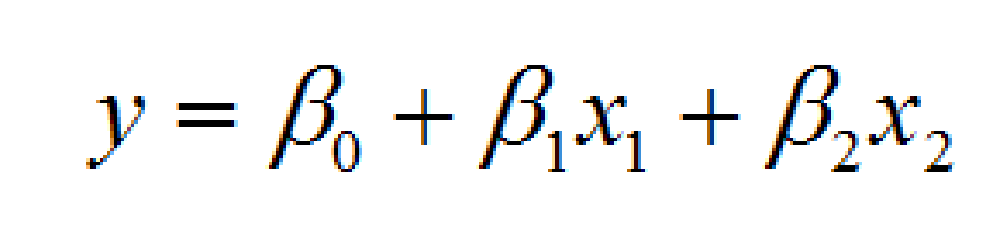
这个模型再简单不过了，模型的解释也可以非常的“白菜话”:
•如果|β1|>|β2|，说明自变量x1比x2重要。因为x1的变化引起因变量y的变化，要比x2更大。反之亦然；
•β0：就是说所有自变量啥都不干（不取任何值），因变量y本身就会体现出的平均水平。例如研究价格和销量关系中的“刚需购买”；
•β1：假设按住自变量x2不动，自变量x1平均每变化β1个单位，因变量y就会平均变化1个单位；
•β2：假设按住自变量x1不动，自变量x2平均每变化β2个单位，因变量y就会平均变化1个单位；
•如果β1非常接近于0，那说明这个自变量x1对整个模型而言没有啥用处，因为无论它取什么值，和一个无穷小的数β1相乘，结果还是无穷小。
•……其他

以上尽管以线性回归为代表的统计模型可解释性强，但一直以来很多人都没将之纳入法眼。一方面是太简单了，体现不了“学术水平”；另一方面就是和“黑盒子”相比偏差大了些，怕同行取笑或者被导师打回去文章重写。我也自我批评一下：我曾经参加论文答辩时，看到有同学3万多字的论文中，居然只用了一个多元线性回归时，还一度觉得他不会是太偷懒了，拿个这么简单的模型来凑字数吧。不过这次看了钟院士团队的论文后，我倒是非常的受启发。

 一、虽然线性模型本身拟合偏差比“黑盒子”大，但是它有很多高级版本的应用场景，你不知道而已
就拿特征工程中，高价值的流程节点是如何解决共线性的问题。如果解决了共线性，在保证不降低预测精度的同时，一方面可以降低过拟合的风险，另一方面提取的特征少了（自变量），模型的计算量和模型对计算资源的耗费，将会大幅降低。本次钟院士团队采用的是广义线性回归中的LASSO回归（Leastabsolute shrinkage and selection operator），从72个检测指标中提取出了19个和COVID-19重症高度相关的指标；接下来在Logistics回归模型中，再次提取出了10个关键指标，作为重症患者的独立统计预测因子，纳入到风险评分工具中。

具体的指标见下表（医学术语翻译的可能不够准确，请学医的读者见谅）

在这里说到的LASSO回归，就是线性回归模型中，若存在多重共线性场景下，选择显著影响的自变量的方法。在这里论文并没有直接拿它来做COVID-19检测指标的回归分析，而是通过LASSO来做了一次特征工程，过滤掉了很多共线性和不显著影响的自变量指标。 这点确实让我眼前一亮。说实话，很多经典的非监督学习，例如相关系数矩阵、主成分分析法PCA、聚类分析、K-MEANS，逐步回归……都可以实现识别多重共线性的问题。但问题是你识别出了一组高度相关的指标，之后呢？比方说你发现了X1，X2，X3存在共线性问题，你该挑选哪个？过滤掉哪些个？这就是选择上的难题！LASSO回归刚好解决了这个难题。有兴趣的读者可以继续阅读LASSO回归的原理介绍和在钟院士团队论文中的应用。

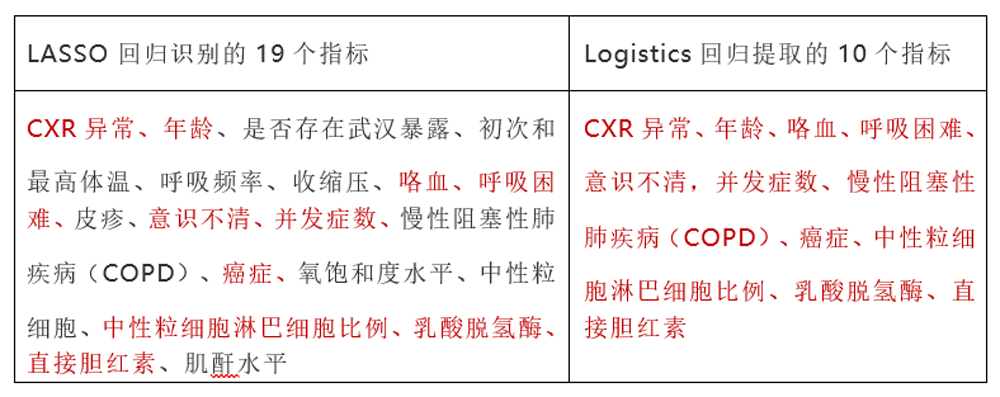
LASSO回归的原理，其实不是很复杂，之所以说它是线性回归的高级版本，实际上是有原因的。LASSO回归是Elasticnet模型家族理论中的一个特殊场景，它有一个同胞兄弟，叫作岭回归（Ridge回归）

一般的线性模型，为估计出模型系数的β向量，是对以下的残差平方和RSS求极值而来。

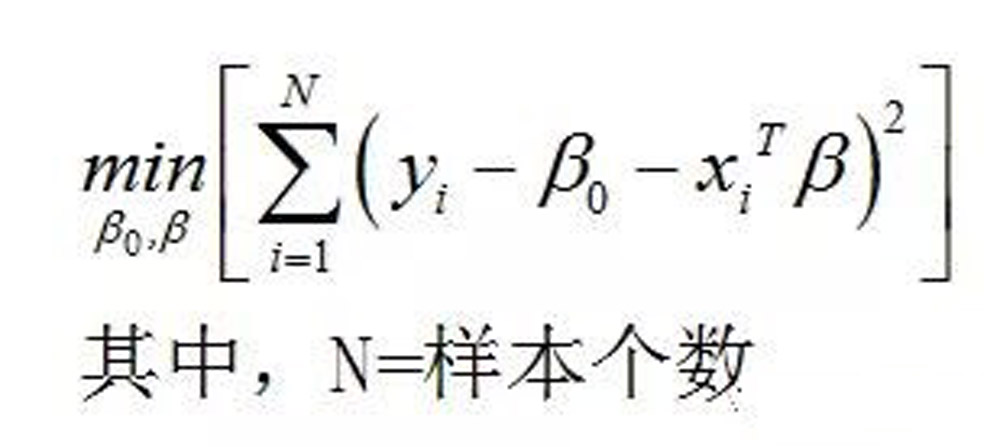
因为上面的残差平方和对于β来说是一个二次函数，是一个高维度的抛物面而且开口向上，因此存在着值。为了能够画出来，我假设β向量只有2个元素，那么RSS就是一个三维抛物面。它本身及的平面投影示意图如下：

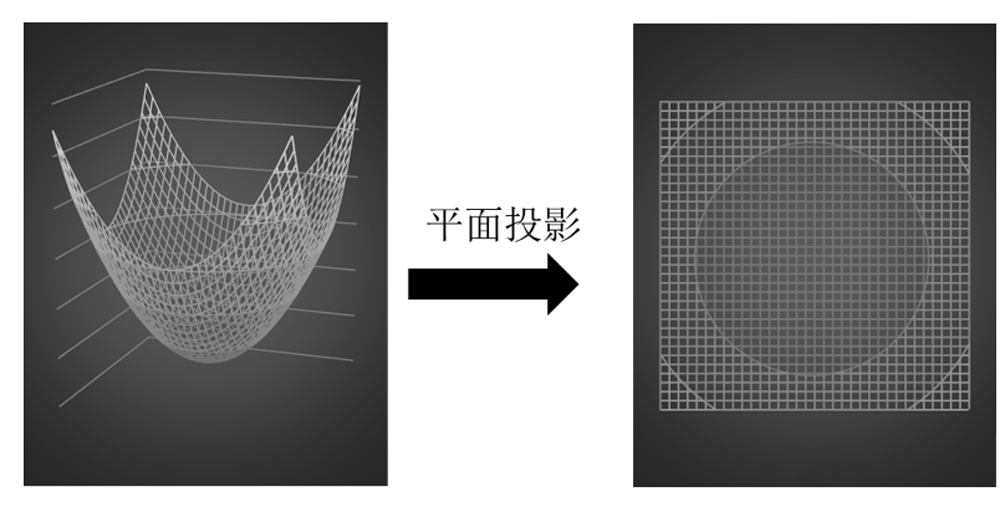
想要求出β向量中的那两个的无偏估计值，只需要对RSS求β的一阶偏导，然后让其为0，接下来就可以求得解析解。但是如果β向量中存在着自变量的共线性，那么上一步计算的表达式中（如下）

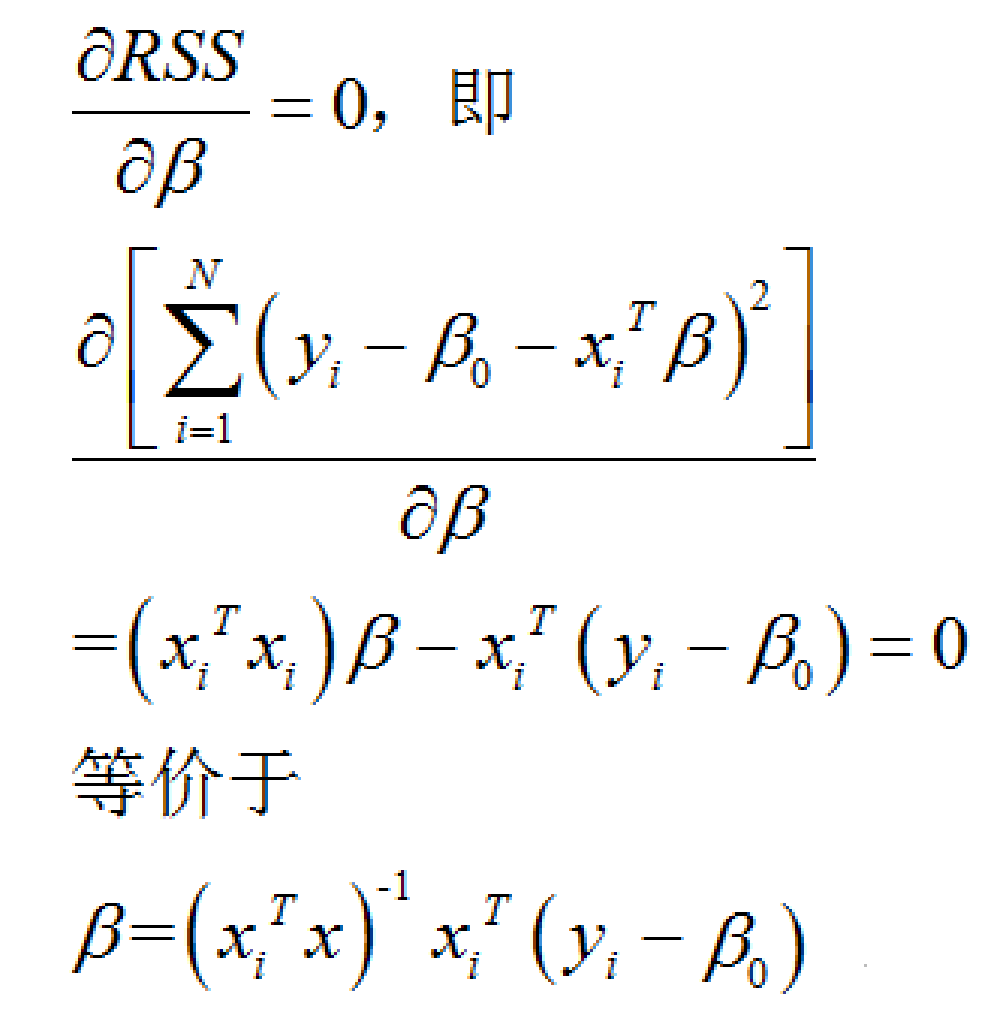
β有解的充分必要条件rank(XTX)必须是满秩就不成立。或者即便成立，但由于自变量之间高度线性相关，行列式XTX非常接近于0，那么得到的β解就非常不稳定。

这时候，就需要对RSS加入约束条件，或惩罚项。

Elastic net 模型家族是这样给RSS小化添加约束条件的

当上式α=0时，小二乘线性回归就变成了岭回归，此时β向量中所有的元素，也就是模型的系数都保留，但是各个自变量之间通过相互借用影响强度（borrow strength from each other）来保证所有的系数都不为零；
当α=1时，则变成了LASSO回归，此时将会将一些影响力高的自变量保留，影响力不大的则让其系数为0。
 
这个时候RSS优化使用约束条件，用几何表示就是这样：
还是二维空间的例子，由于|β|中只有2个元素，因此|β|是一个正方形，它和RSS在相同平面上有一个投影交集，就是下图中红色曲线的交点。这个交点对于|β|来说更容易出现在坐标轴上，因此β向量就不必全部取值，只需要取一个就行，另一个就是0。这样就实现了自变变量的选择和过滤。

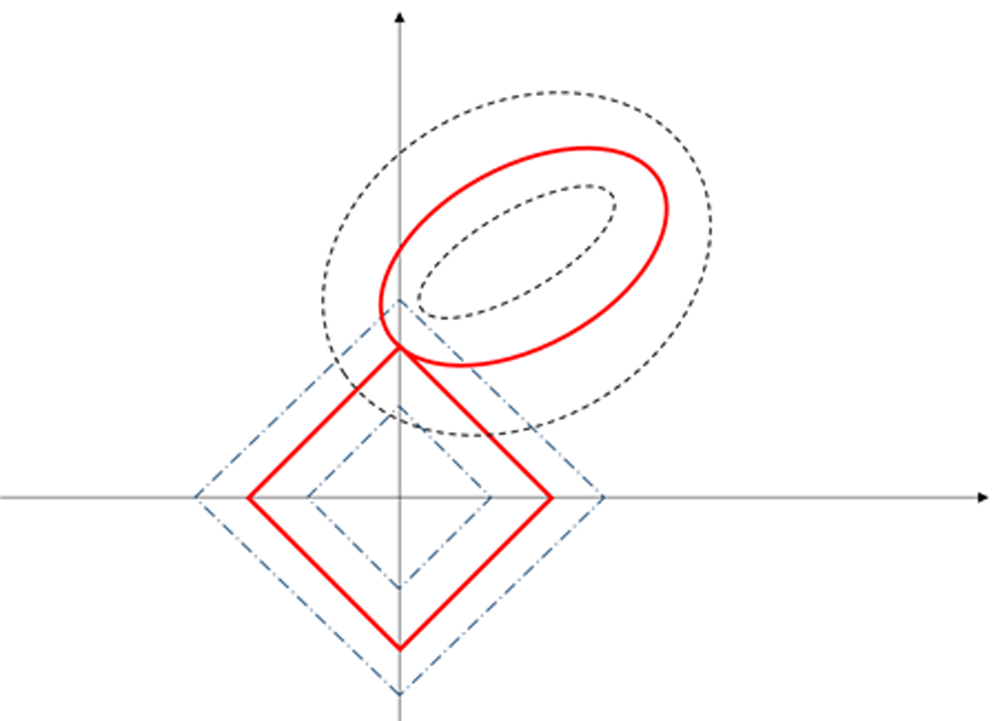
接下来，可以通过设对下面的RSS进行求解极值就可以得到β向量的值。

由于λ的取值越大，对于整个RSS的极值求解来说就会增加约束条件的难度，因此会被过滤掉更多的自变量。因此，需要借助计算机软件对λ进行逐步迭代试算，找到比较合适的λ值。

在钟院士团队的论文中，提到了R软件的包glmnet，团队通过这个开源的包进行重症病患预测因子的过滤。

通过观察论文中λ-系数轨迹图，我们可以看到，当λ迭代到一定程度，例如log(λ)=-5或-6时，一些不重要的变量的系数全部收敛到接近于0，此时剩下的变量的系数依然有比较显著的非零特性。而刚好这些剩下变量就是之前评分中的那些检查指标（这个结果是利用Logistics回归中的LASSO选择结果，因此剩余的系数个数刚好是10个）。

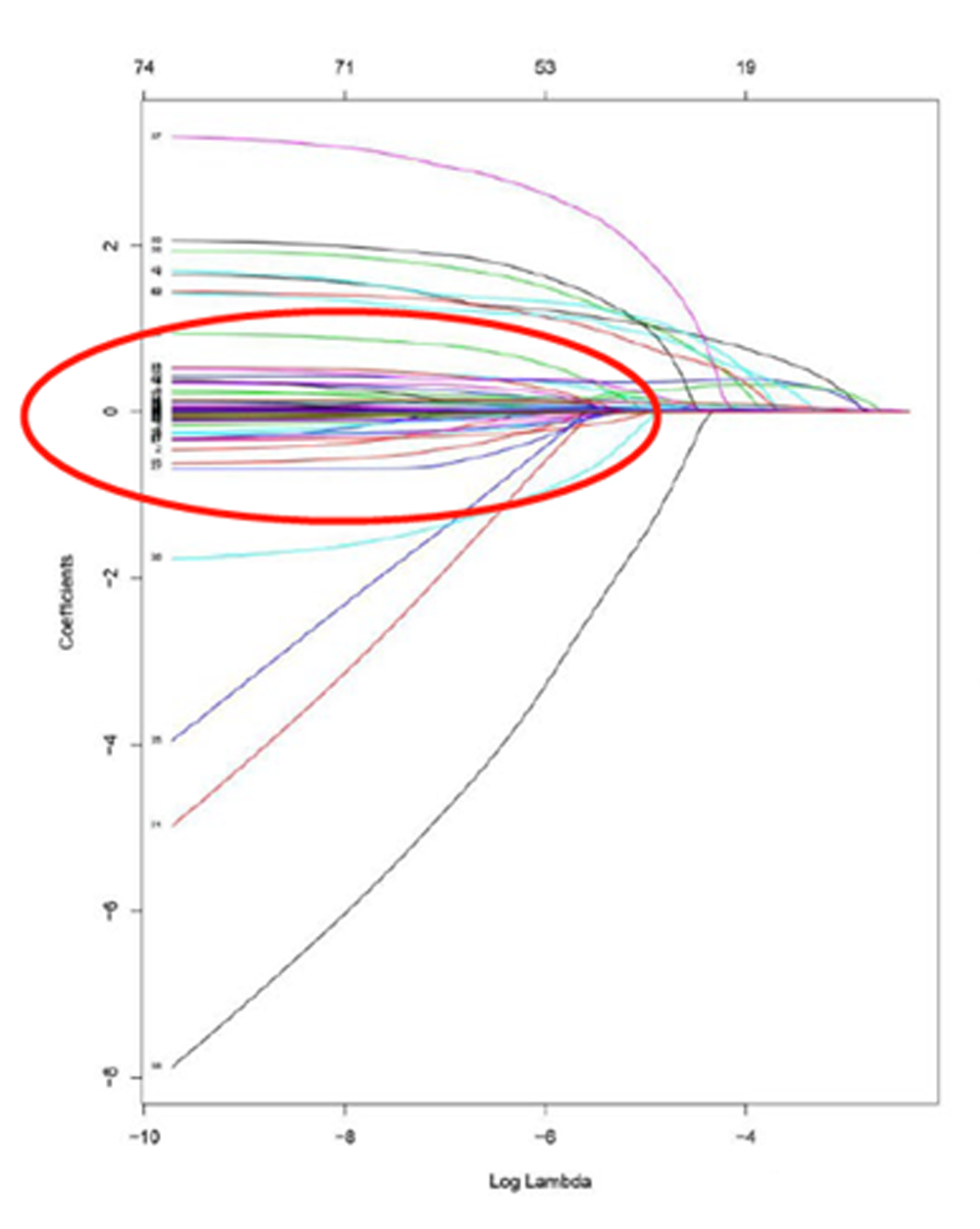
而当0<α<1时，β向量的结果介于岭回归和LASSO回归之间。

二、对于治病救人而言，模型的使用更应该侧重于可解释。

这一点也是本次论文给我的启示。

其实模型可解释在我日常工作中也经常遇到这样的场景：
辛苦搞了几个模型出来，在平衡预测精度和可解释时，往往很难拿捏。于是乎就选择了“黑盒子”与“可解释”中各挑一个模型，然后加权平均。如果客户也是和我一样是分析师圈子的人，那么他可能就会偏向于“黑盒子”、而若客户是偏业务的人，那么就会更偏向于“可解释”。我还依稀记得客户问我，什么是模型系数的显著性水平、模型的现实意义是啥……这些记忆片段。由于我平时的工作还不涉及到治病救人这么事关人命的大事，因此这种平衡方法使用也就没什么大碍。但是对收治的病人并进行重症的预判，则是一件人命关天的大事儿，来不得半点“讲不清楚，反正就是预测效果好”。另外，我觉得模型选择侧重于可解释，主要还有一个重要原因：

就本论文而言，这个重症评分工具的推广对象，是全社会各级医疗和疾控机构，大家的水平层次都是参差不齐的。当工具的使用对象是只具备基础医疗训练的基层医务人员时，你搞一个难以解释的“黑盒子”，又还要他们懂得设定参数和超参数，这样就会造成基层医务人员的困惑，甚至不知道怎么用，也就难以推广。另外，一些普通老百姓也会看到这个工具，当然有条件自检的话，同样也可以自己使用。如果让普通人去调整这么复杂的模型，这个工具自然就会被敬而远之，起不到造福百姓的作用了。

数据分析应用技能之Python试听课

https://www.cpda.cn/coursedetail/?id=56

 

数据分析应用技能之R语言试听课

https://www.cpda.cn/coursedetail/?id=55

 

运筹学解读数据集训营试听课

https://www.cpda.cn/coursedetail/?id=44

 

SPSS核心技能速成班试听课

https://www.cpda.cn/coursedetail/?id=49

 

CPDA数据说第十九期《CPDA开创数据分析行业全新教学模式》

https://www.chinacpda.com/dongtai/20984.html

 

数据科学、大数据与数据分析

https://www.chinacpda.com/jishu/20921.html

 

更简单直接的了解下数据科学家

https://www.chinacpda.com/wenti/20809.html

 

盘点哪些运营使用的数据分析工具

https://www.chinacpda.com/jishu/20674.html

 

数据可视化一个选择显示数据的方式

https://www.chinacpda.com/jishu/20585.html

 

查找您周边省份授权培训中心：

https://www.chinacpda.com/train/

 

2020年CPDA数据分析师线上报名：

https://www.chinacpda.com/baoming.php

 

数据分析师的职业规划：

https://www.chinacpda.com/career/

 

CPDA数据分析师考核时间：

https://www.chinacpda.com/examine/

 

免费客服热线：400-050-6600

商业联合会数据分析专业委员会