现在我们来看一下本次分析需要用到的数据：

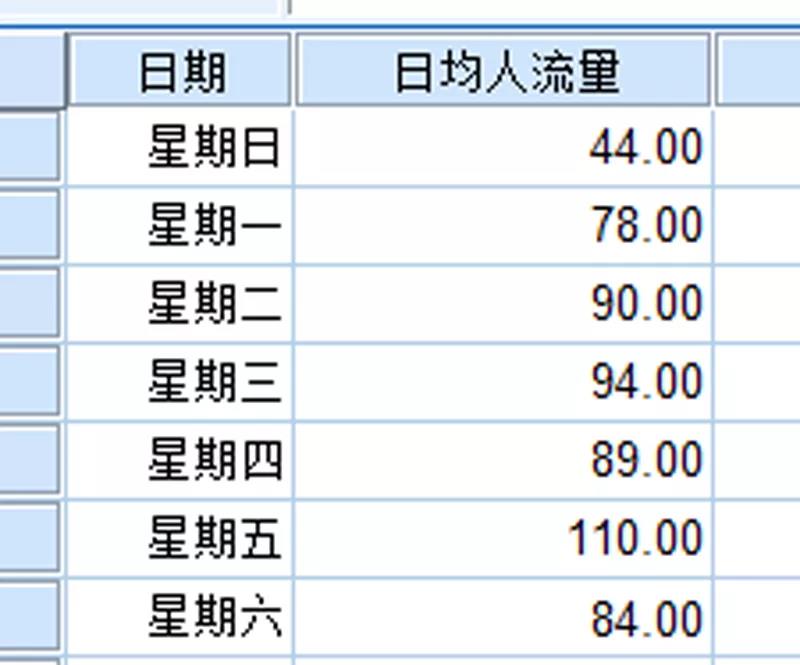
上图中的数据是某个医院的人流量相关数据，我们需要对一周内的日均人流量进行分析，了解是否一周中每天的病人流量是相同的。
在进行分析时，我们首先要对日均人流量数值进行加权处理：

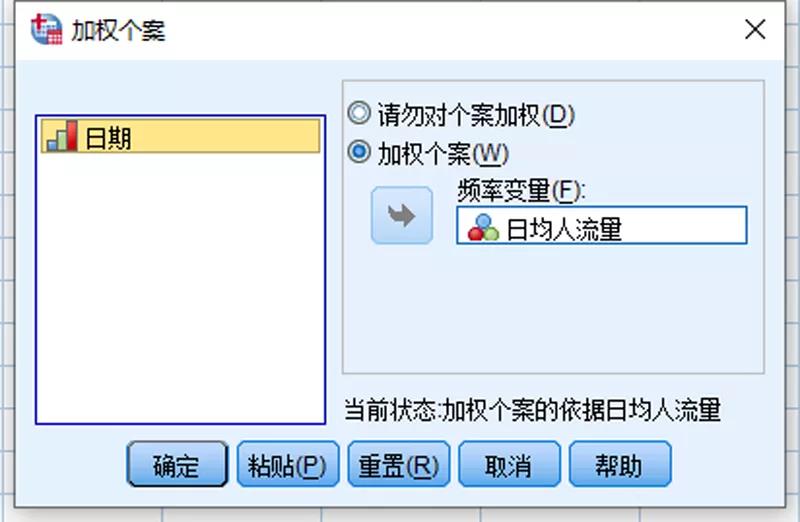
然后我们选择非参数检验中的单样本：

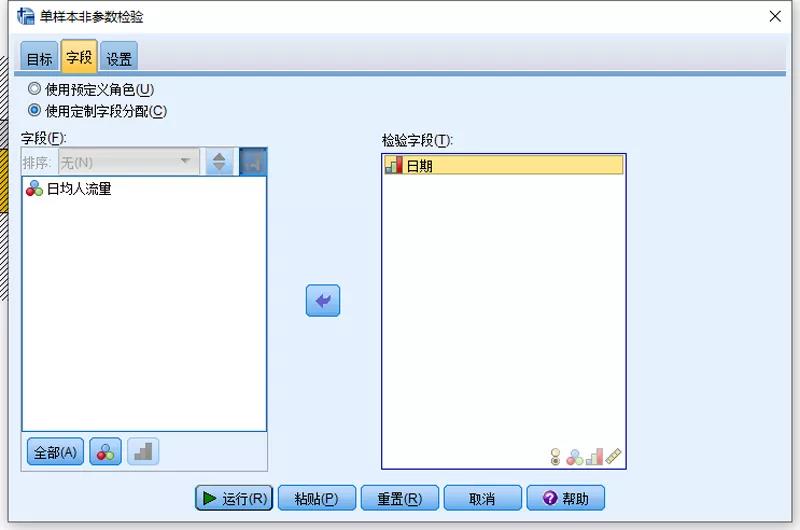
我们在字段选项中将日期选入检验字段中，设置选项中选择卡方检验。我们点击运行即可得出本次分析的结果：

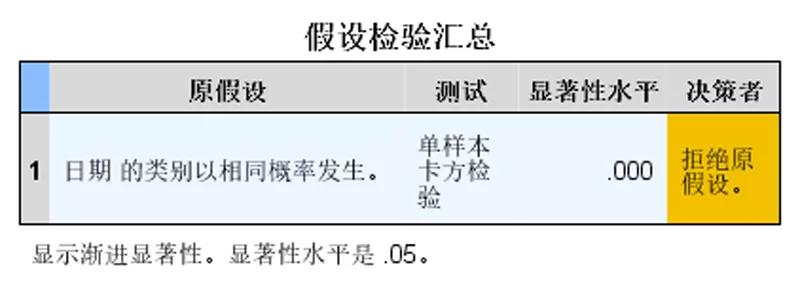
在结果中我们可以看到本次检验的原假设、检验方法、显著性水平P值以及的决策。本次分析中显著性P值为0.000，小于显著性水平0.05，说明一周中每天的人流量是不一致的。
我们双击结果图，可以进入到模型中看更加详细的分析结果：

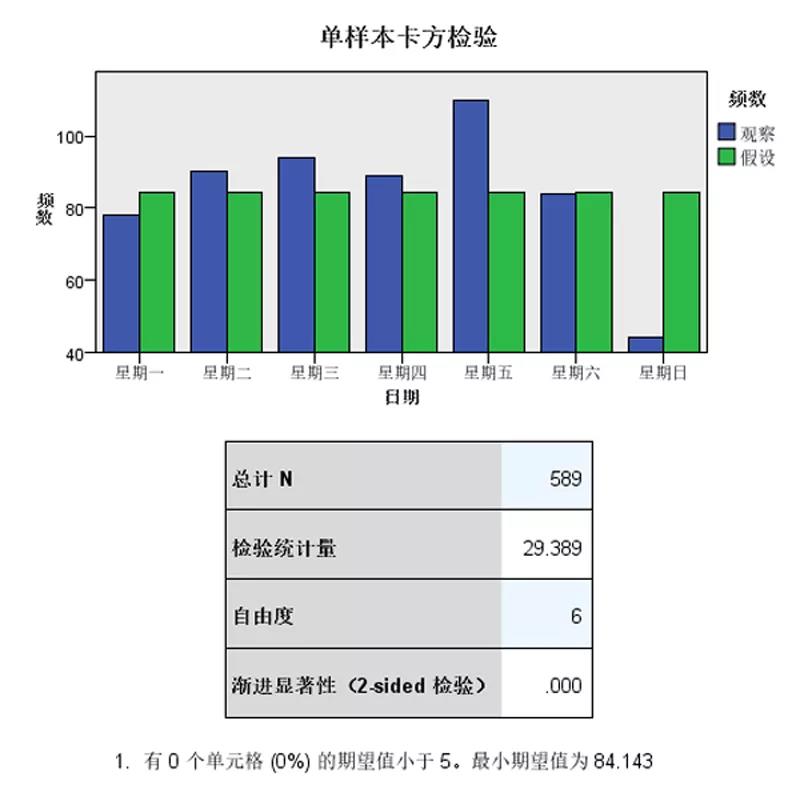
从上图可以看到，卡方统计量为29.389，显著性P值为0.000，小于显著性水平0.05，说明通过了显著性检验，也就是说一周中每天的人流量有显著差异。同时我们还可以看出在周五的时候人流量多，周日的时候人流量少（周末医院门诊较少，人流也会降低），其余几天的人流量差别不是特别大。

还有一点需要大家注意的是当我们进入到模型中以后，我们还可以通过把鼠标放在聚类条形图上来了解各个字段具体的频率及差别（残差）。