如何使用数据分析技术进行销售预测
来源:广西CPDA数据分析师 / 作者:陈虹坚 / 时间:2020-06-23
在我们的日常工作中,有很多时候,都需要对明年的销售额进行预测,以便进行费用、资金及资源的安排。如何对次年的销售额进行相对合理的预测,相信是市场运营人员及管理者关注的问题。本文通过一个例子,介绍如何使用数据分析技术,对次年的销售额进行预测。
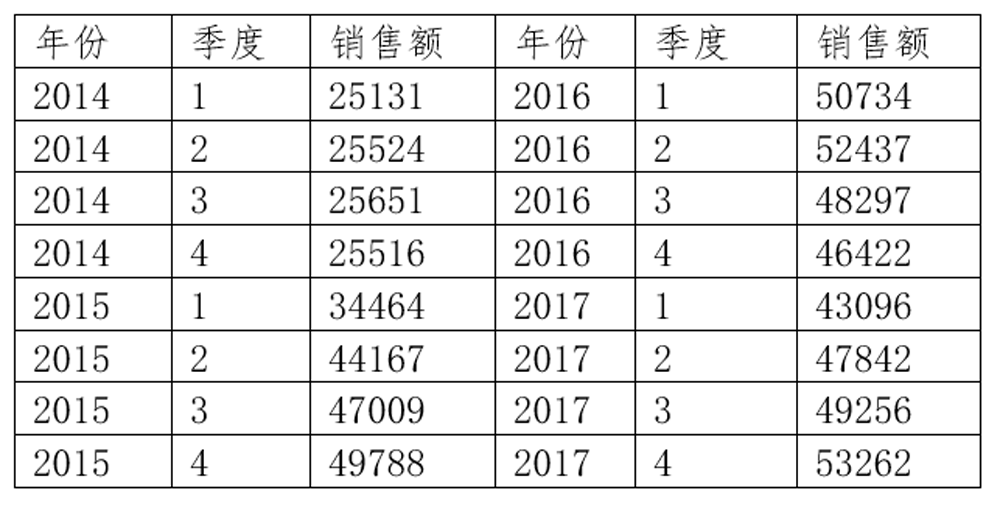
下表为A公司2014-2017年每个季度的销售额,现需要对该公司2018年的销售额进行预测,以便管理者安排运营资金、资源及进行绩效考核目标设定。
二、业务分析
经过分析,A公司的产品销售有以下几个特点:
1.销售有淡旺季之分
每年的4-5月、10-11月为销售旺季,除此之外,每年春节、五一、十一等长假也会出现销售高峰;
2.呈现明显的周期变化
该产品每年的每个季度销售特征都非常明显,一季度春节期间销售额达到一个高峰,二季度因国际大环境影响4-5月达到第二次销售高峰,三季度天气炎热为全年销售低谷,四季度随着十一长假及国际大环境影响又迎来一个销售高峰,次年周而复始。
3.因市场及政策因素导致销售的不确定性
该产品有可能会受到政策调整、市场大环境及其他不确定因素的影响,导致销售额呈现不规则的波动。
4.长期的趋势
该产品从长期趋势上看,呈现向上增长的态势。
结合上述对A公司产品销售额的分析,我们需要根据该产品历史的销售数据,结合产品的特点,来预测它未来的销售额。可以采用时间序列预测的季节分解法来对该产品下一年度的销售额进行预测。
三、分析模型
结合上述业务场景,A公司产品销售时间序列主要由四个影响因素构成:长期趋势,用T表示;季节变化,用S表示;周期变化,用C表示;不规则变化,用I表示。
我们设销售额为Y,那么Y即可看成是T,S,C,I的函数,即Y=f(T,S,C,I),此时只需要确定f的表达式,并且从Y中把T,S,C,I分离出来,那么如果T,S,C,I的变化是已知的,即可对Y进行预测。
根据A公司的产品业务特点,本例时间序列应用乘法模型,即 Y = T×S×C×I。
四、预测步骤
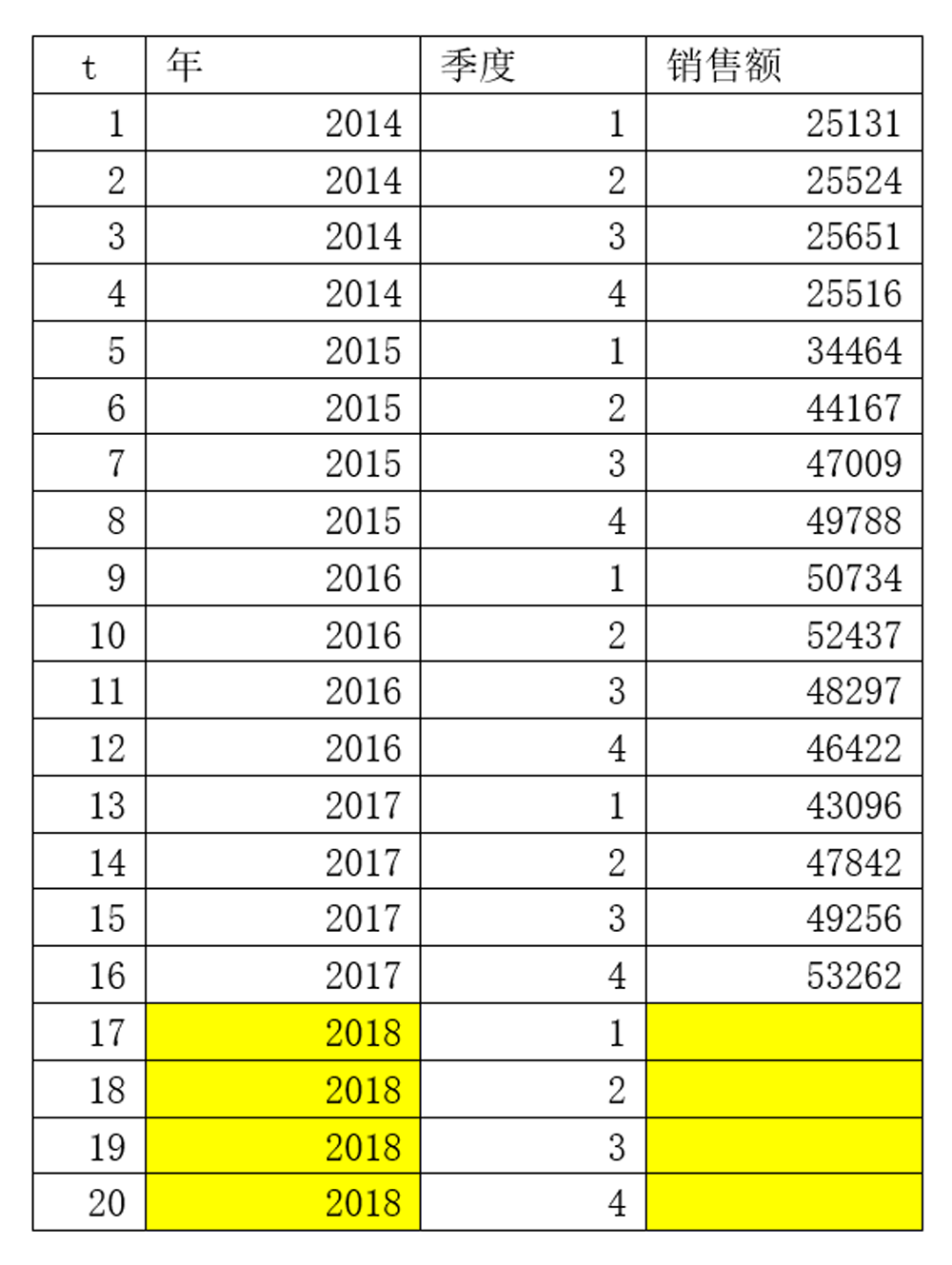
1、给变量t赋值;
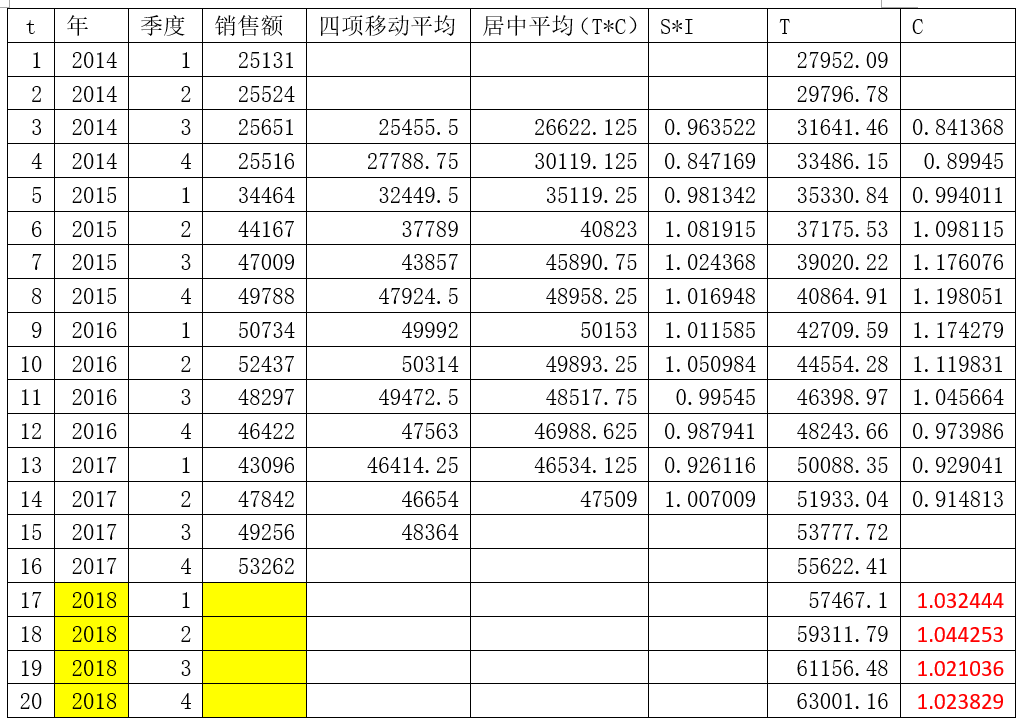
按照时间的顺序,给现有的历史数据及需要预测的数据进行赋值,如下表所示。表中17-20序列即是需要求出的2018年四个季度的预测数据。
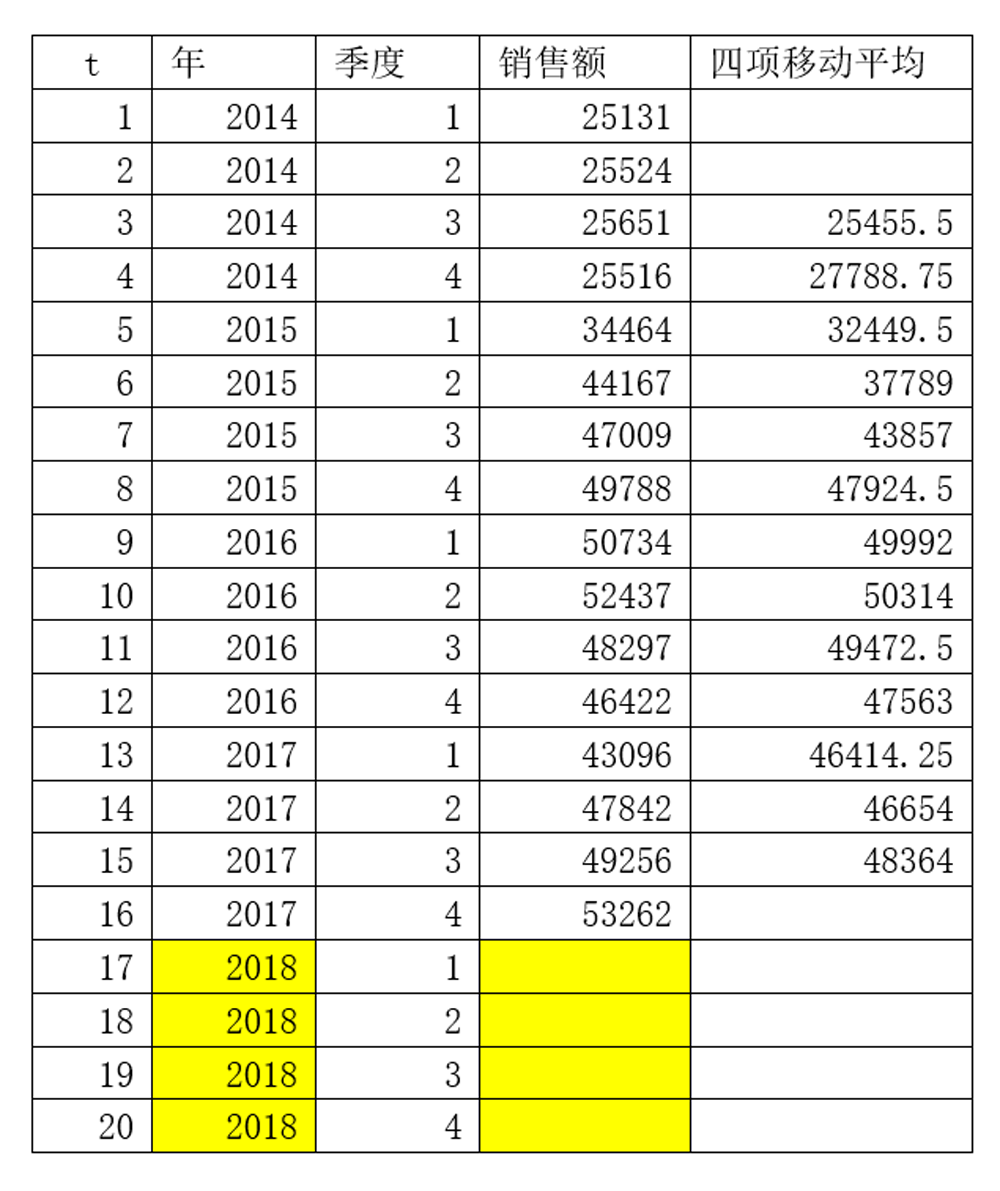
2、剔除季节变化;
因为我们的历史数据是按季度呈现的,一年之内变化四次,为了剔除一年之内的波动,需要对数据进行四项移动平均。
四项移动平均后,提出了一年之内的季节变化和不规则变动,即剔除掉了S×I。
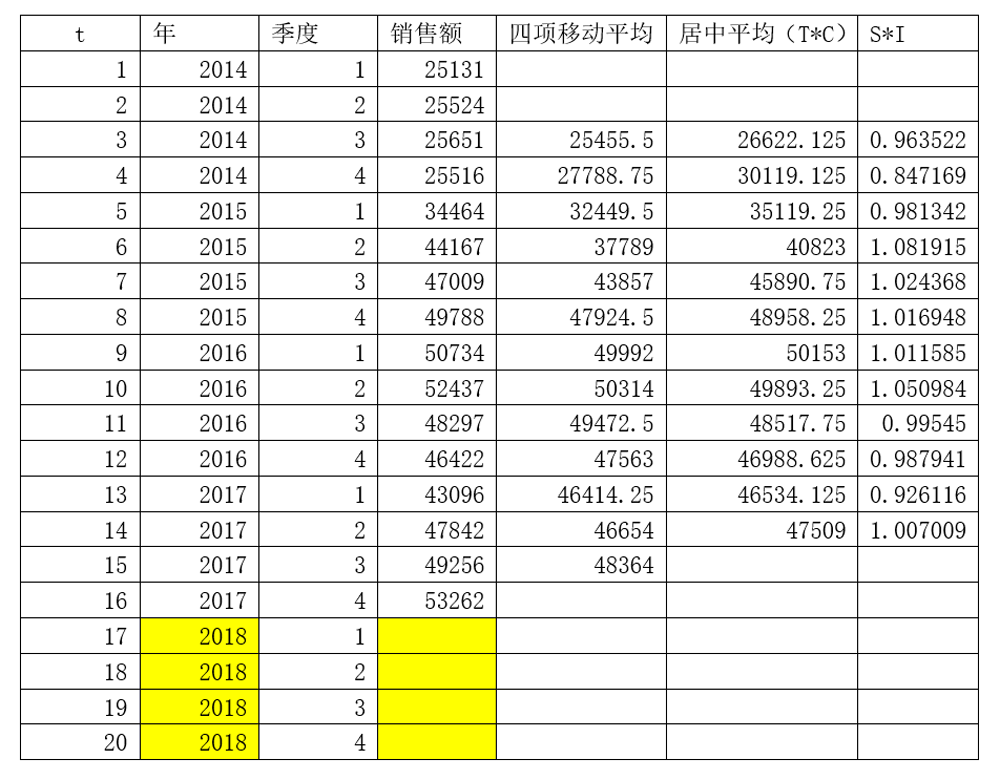
3、求出T×C;
我们在上一步骤剔除了S×I后,得出的结果还不是T×C,因为在四项移动平均中,我们已将相邻的4个数据相加取平均得到一个值,表中2014年的四个季度的数据被平均时,它们的平均数应该置于2.5的位置,第二个数应放在3.5的位置,其余数据取平均时也有类似的问题。因此我们需要再做一次居中平均来解决这个问题,如下图所示。完成居中平均后,得到的结果就是T×C。

4、求S×I;
因为Y = T×S×C×I,因此S×I=Y/T×C,上一步骤中,我们已经求出T×C,带入上述公式即可得到S×I,如下表。
5、求T和C;
模型中T表示长期趋势,根据业务背景,A公司的产品销售额从长期趋势上看,是呈上升态势的,因此它是一条反映增长趋势的直线,即T=A+Bt,可以用线性回归的方法求出T,如下图所示。
SUMMARY OUTPUT


有了T的值后,因为T×C已知,根据模型Y = T×S×C×I,我们即可求出C的值,如上图所示。由于我们需要求出17-20的C值,则需要根据现有数据,结合业务特征,拟合出一条波动的曲线,得到C在17-20序列的值。
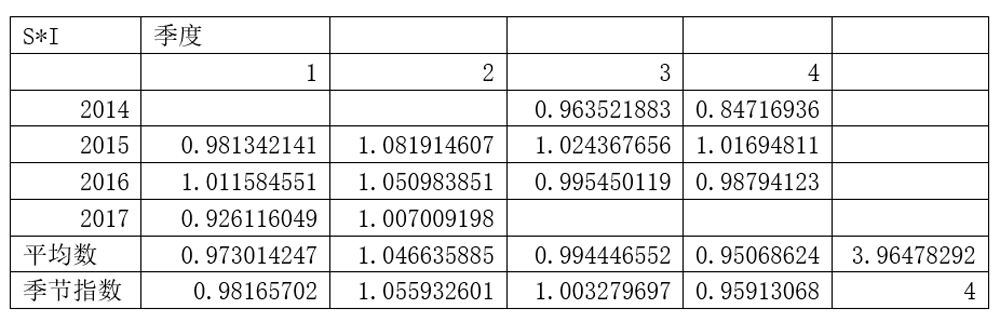
已知S×I的值,可以将S和I分别分离出来。S表示季节变化,不同的年份,季节的值应该都是相同的,但我们看下表,同样的年份同样的季度,值并不相同,原因就在于I的影响。为了消除I的影响,我们对不同年份,同一季度的值进行平均。同时,模型中季节因素对Y无影响则四个季度之和应该为4,否则需要进行修正。按等比例原则,修正后的积极指数如下表所示。
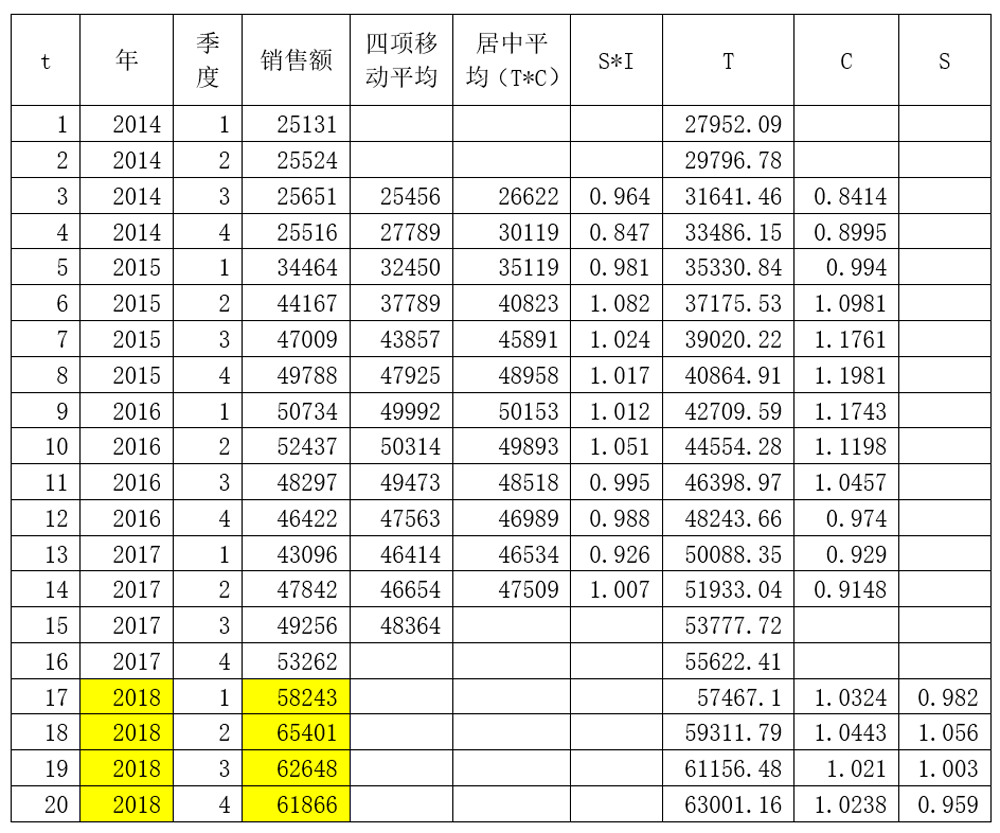
7、运用模型预测
我们分别求出了T、S、C的值,根据乘法模型,即可得出2018年每个季度的预测值,计算结果见下表。
五、结论与建议
季节分解法的计算思路为时间序列是由时间t和根据时间变化的Y构成,Y由T,S,C,I即长期趋势、季节变化、周期和不规则变动构成,根据乘法模型Y = T×S×C×I,只需要分解T,S,C,I即可求出预测值。同时,任何的数据分析方法都需要与业务特征、行业特点相结合,才能更好得利用数据分析这个工具来解决业务问题。












