什么叫间隔量表

测量间隔刻度是一种测量刻度，其特征是刻度单位之间的间隔相等。

间隔刻度的一个示例是用于测量，标尺由相等的单位组成，使用区间标度，您不仅知道不同的值是大还是小，而且还知道它们的大小是多少。

CPDA对于比例量表的解释

测量的比例尺是一种测量尺。它的特点是刻度单位之间的间隔相等，并且小刻度值为零。

物体的重量就是比例尺的一个例子，小值为零，因为静止的物体可以失重，但不能具有负重量。

CPDA数据分析师如何解释相关系数

相关系数的符号和 值描述了两个变量之间关系的方向和大小。

在CPDA数据分析师课程中相关系数的值在-1和1之间。

数据分析相关系数的值越大，线性关系越强。

强的线性关系由-1或1的相关系数表示。

弱的线性关系由等于0的相关系数表示。

正相关表示如果一个变量变大，则另一个变量趋于变大。

负相关表示如果一个变量变大，则另一个变量趋于变小。

CPDA数据分析积矩相关系数仅测量线性关系。因此，相关性为0并不意味着两个变量之间的关系为零。相反，它意味着零线性关系。（两个变量可能同时具有零线性关系和强曲线关系。）

散点图和相关系数

散点图显示了不同的数据模式如何产生不同程度的相关性。

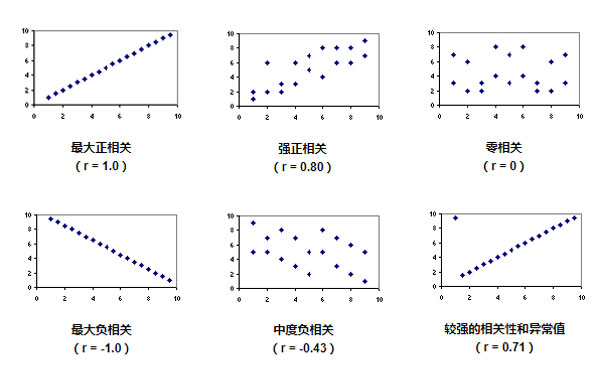
CPDA数据分析师学员可以从散点图可以明显看出几点

当图中直线的 斜率为负时，相关为负；反之，则为负。反之亦然。

当数据点恰好位于一条直线上时，会出现强的相关性（r = 1.0和r = -1.0）。

随着数据点变得更加分散，相关性变得更弱。

如果数据点属于随机模式，则相关性等于零。

相关性受异常值影响 。比较个散点图和一个散点图。一个图中的单个异常值极大地降低了相关性（从1.00降低到0.71）。

CPDA数据分析师教你如何计算相关系数

如果学员查看不同的统计教科书，则可能会找到外观不同（但等价）的公式来计算相关系数。在本节中，CPDA数据分析师介绍您可能会遇到的几个公式。

下面给出了计算乘积矩相关系数（r）的常用公式。

乘积矩相关系数。 两个变量之间的相关性r为：

 r =Σ（xy）/ sqrt [（Σx 2）*（Σy 2）]

其中Σ是求和符号，x = x i - x，x i是观察i的x值， x是平均值x值，y = y i - y，y i是观察i的y值， y是平均值y值。

下面的公式使用总体平均值和总体标准差从总体数据中计算总体相关系数（ρ）。

人口相关系数。 两个变量之间的相关性ρ为：

ρ= [1 / N] *Σ{[（X 我 - μ X）/σ X ]

* [（Y 我 - μ Ý）/σ ÿ ]}

其中，N是在人口观测值的数量，Σ是求和符号，X 我是用于观察i中的X值，μ X是总体平均值为变量X，Y 我是用于观察在Y值i，μ ÿ被总体平均值为变量Y，σ X是X的总体标准偏差，σ ÿ是Y的总体标准偏差。

以下公式使用样本均值和样本标准差从样本数据计算样本相关系数（r）。

样本相关系数。 两个变量之间的相关性r为：

r = [1 /（n-1）] *Σ{[（（x i - x）/ s x ]

* [（y i - y）/ s y ]}

其中n是样本中的观察次数，Σ是求和符号，x i是观察i的x值， x是x的样本均值，y i是观察i的y值， y是样本均值在y中，s x是x的样本标准偏差，而s y是y的样本标准偏差。

样本相关系数的解释取决于样本数据的收集方式。对于大的 简单随机样本，样本相关系数是总体相关系数的无偏估计。

后两个公式均可从个公式导出。当您拥有整个总体的数据时，请使用个或第二个公式。当您仅具有样本数据但要估计总体中的相关性时，请使用第三个公式。如有疑问，请使用个公式。

幸运的是，您几乎不需要手工计算相关系数。许多软件包（例如Excel）和大多数 图形计算器 都具有关联功能，可以为您完成这项工作。

查找您周边省份授权培训中心：

http://www.chinacpda.com/train/

2020年CPDA数据分析师线上报名：

http://www.chinacpda.com/baoming.php

CPDA数据分析师在线学习班正式启动:

http://www.chinacpda.com/data/detail/?id=623

为您带来不一样的课堂，一样的精彩:

http://www.chinacpda.com/data/detail/?id=614

免费客服热线：400-050-6600

商业联合会数据分析专业委员会