CPDA数据分析师在对数据进行统计时使用汇总度量来描述一组数据中的可变性或分布量。在数据统计时变异性的常见度量是范围，四分位间距（IQR），方差和标准偏差。

数据分析师定义的范围

在这个范围中在和小值之间的差异 我们来为它设定值。

 CPDA数据分析师举例说明：考虑以下数字：1、3、4、5、5、6、7、11。对于这组数字，范围将是11-1或10。

所谓的四分位间距（IQR）

四分位数间距（IQR）是变异性的度量，基于把一个数据集到 四分位数。

 在数据分析统计中四分位数将等级排序的数据集分为四个相等的部分。数据分析师可以划分每个部分的值称为，第二和第三四分位数；它们分别由Q1，Q2和Q3表示。

 Q1是排名数据集前半部分的“中间”值。

Q2是 集合中的中位数。

Q3是在“中间”值第二秩有序数据集的一半。

四分位间距等于Q3减去Q1。例如，考虑以下数字：1、2、3、4、5、6、7、8。

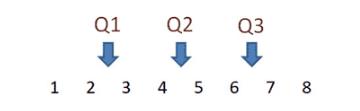
在这副图中Q2是整个数据集的中间值-中间值

这个例子中，数据分析师将得到偶数个数据点，因此中位数等于两个中间值的平均值。因此，Q2 =（4 + 5）/ 2或Q2 = 4.5，Q1是数据集前半部分的中间值，由于数据集的前半部分有偶数个数据点，因此中间值是两个中间值的平均值。即Q1 =（2 + 3）/ 2或Q1 = 2.5。Q3是数据集后半部分的中间值。同样，由于数据集的后半部分具有偶数个观测值，因此中间值是两个中间值的平均值。即Q3 =（6 + 7）/ 2或Q3 = 6.5，四分位数范围是Q3减去Q1，因此IQR = 6.5-2.5 = 4。

 CPDA数据分析师特别提醒：此过程将数据集分为相等大小的四个部分。部分由1和2组成；第二部分，3和4；第三部分5和6；第四部分7和8。

在CPDA数据分析师课程中会详细为学员讲解到，四分位间距的定义不同。它定义为一组数据中间50％的值和小值之差。

要使用此定义计算四分位数范围，请首先从较低的四分位数中删除观察值。然后，从上四分位数中删除观察值。然后，从其余观察值中计算出值和小值之间的差。

Datahoop数据分析师平台不仅提供日常学习和考试练习的环境：

http://www.chinacpda.com/datahoop/

查找您周边省份授权培训中心：

http://www.chinacpda.com/train/

2020年CPDA数据分析师线上报名：

http://www.chinacpda.com/baoming.php

免费客服热线：400-050-6600

商业联合会数据分析专业委员会