CPDA数据分析师在回归中，当自变量对因变量的影响根据一个或多个其他自变量的值而变化时，他们之间存在交互作用。

有关数据分析方程中的互相作用效应

在CPDA数据分析师回归方程中，交互作用表示为两个或多个自变量的乘积。例如，这是一个没有交互作用的典型回归方程：

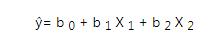
CPDA数据分析师会这样理解：这个方程中ŷ是因变量的预测值，X 1和X 2是自变量，b 0，b 1和b 2是回归系数。

数据分析师在为你举个其他例子：例如这是具有相互作用的相同回归方程：

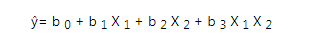
通过CPDA数据分析师看来，b 3是回归系数，X 1 X 2是相互作用。X 1和X 2之间的相互作用 称为双向相互作用，因为它是两个自变量之间的相互作用。

高阶交互是可能的，如以下等式中的三向交互所示：

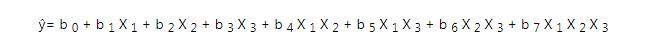
CPDA数据分析师在遇到此现象时，通常会避开诸如X ₁ X ₂ X _3之类的高阶交互，因为它们不太好解释。

在数据分析中交互作用图是显示独立变量之间交互作用存在或不存在的线形图表示方法。如果CPDA数据分析师要创建交互图，可以根据下面的操作来很快的实现：

1、数据分析师要在垂直轴（即Y轴）上显示因变量；在水平轴（即X轴）上有一个自变量。

2、CPDA数据分析师针对潜在相互作用变量的每个级别分别在因变量上绘制平均得分。

3、我们可以连接均值，为交互变量的每个级别分别生成线的方式。

4、学员如果要了解潜在的交互作用影响，请比较交互作用图中的线条：

 如果我们得出的线是平行的，这就表明没有相互作用。

反之如果线不平行，这样就很明显的存在相互作用。

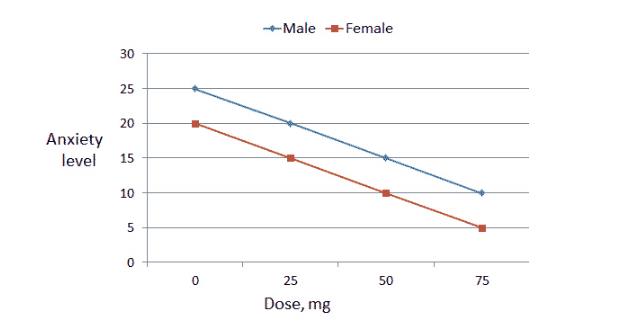
CPDA数据分析师举例说明，假设我们的企业开发出一种治疗焦虑症的药物。因变量是焦虑（绘制在Y轴上）。自变量是剂量（在X轴上绘制）。CPDA数据分析师可能会根据性别来假设一种互动效应。我们为了可视化潜在的相互作用，数据分析师将按性别绘制每个剂量的平均焦虑评分，并将均值与直线相连，如下所示：

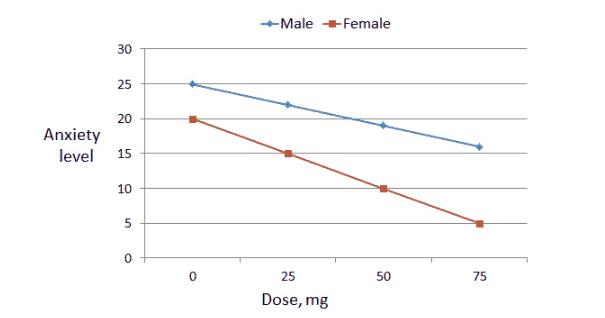
在上面的假设交互图中线不平行，女性的路线表现得更加陡峭，这张图就反映出可能存在基于性别的互动效应，从这幅图中数据分析师将得到的分析结果，该药物对女性的缓解焦虑作用比对男性更有效。

CPDA数据分析师在线学习班正式启动:

http://www.chinacpda.com/data/detail/?id=623

查找您周边省份授权培训中心：

http://www.chinacpda.com/train/

2020年CPDA数据分析师线上报名：

http://www.chinacpda.com/baoming.php

免费客服热线：400-050-6600

商业联合会数据分析专业委员会