近全国上下都在和NCP做斗争，这次也通过参与了“抗疫”的全民战争，使我懂得了很多过去没怎么重视，但是却非常重要的道理。同时也对目前的一些措施有更深刻的理解。

道理，一般分两种层面的理解，一种是定性的理解，简单说即是你知道做什么事是对的，从逻辑上理解为什么是对的；另一种是定量的理解，就是说你明白了做什么事是对的，也明白这件事做到什么程度，相应“做对”的效果有多大。

比方说这次全民对NCP这类抗呼吸道“传染病”，从定性的角度来看，我认为是包含着如下这些道理：

      对抗“传”：就是切断和阻塞疾病的传播途径，例如“封城”、“社区交通管制”、“14天的隔离”、“戴口罩”，“勤洗手”…….，这些是为了切断病毒携带者（包在括潜伏期内）把疾病通过人体移动、飞沫、体液等载体“传”出去。

对抗“染”：譬如说这段时间宅在家也别只是吃喝追剧，要多做些室内健身运动；多喝一些有预防作用的“凉茶”；科研机构也紧锣密鼓的开展研发疫苗……这些措施都是为了增加人的抵抗力，降低万一被病毒接触造成的被感染可能。

对抗“病”：就是研发出治疗NCP的药物，无论是中药还是西药。总之就是尽快将病人治愈，或者降低被感染者的死亡率。

上面这些道理，有一些是从小到大爸妈耳边叮铃、老师嘴上唠叨，耳朵都听出茧了的。

我当然知道做这些措施是可以抵抗传染病，而且有些我也正在做。

但是有时候就是搞不明白，我认真去做和我应付去做这些事儿，区别有多大？

难道就只是影响自己健康而已，或者就只是影响一个社区？

我戴上普通的口罩，和没带口罩相比，当然我知道被感染的风险降低了，但是这对我周围的人的影响到底有多大？

专家们说的R₀＞1和＜1背后有什么更深一层内容？

……

等等很多疑问，在我这段时间宅在房间里认真看了几个传染病的模型后，很多都已经茅塞顿开，甚至感到惊叹！

原来从定量的层面去理解这些“道理”，能比定性的理解有更深刻的印象！

下面就和大家分享下我的心得：

一、首先看简单的传染病模型

 把这个模型看懂了，也就能从另一个角度了解为什么说一旦传染病爆发，感染人数是呈指数级增长了。

简单的指数级增长比较容易理解，比方说今天1个人得病，假设每次只传染1个人，那么初始第0天1个病人，第1天就2个人病人，第2天就4个病人、第3天就8个人，第n天就2ⁿ……个人得病。

这个刚好是一个指数函数，底数为常数2，变化的是它的幂。

不过在传染病研究领域，指数级的增长是从另外一个视角来看

 我们假设在某个时点某个区域内，不考虑出生和其他原因的死亡；也不考虑外部环境对传染病的干预；不考虑人口流动；潜伏期也可以传染；这种病无法治愈；时间的计量刻度是按照天。

初始化一些模型的变量

t时刻的易感染者（Susceptible）人数，用符号S(t)表示；

t时刻的被感染者（Infective）人数，用符号I(t)表示；

每个被感染者每天有效接触且足以使人致病的人数为λ，这些λ均为健康的人，那么每天新感染的人数就是λI(t)

建立模型：

(1.1)式的模型左边和右边同时除以Δt，当Δt→无限小或0时，就会得到导数的定义式

然后以此建立微分方程

解这个微分方程。个式子容易看出是一阶线性微分方程，根据解这类微分方程的方法容易得到该方程的解I(t) = I₀e^λt。

I₀e^λt 也就是被感染者的数量随着时间推移的变化规律。

看到这个常数e了吗，以及e右上角的幂是不断增大的，也就是为什么被传染病领域说的感染的人数的增长是指数级了。

e的幂增长速度和直线比那是很快的，从这个简单的传染病模型我们可以看出，只要随着时间的推移t→∞，I(t) →∞，也即是终世界上全部健康人都会被传染。

 被感染的人的数量是不是只根据一种指数级增长而变化呢，其实不是的。

解决传染病感染人数增长快慢还有一个的关键就是λ，也就是控制已感染者接触健康人的数量，让这个值越小越好。

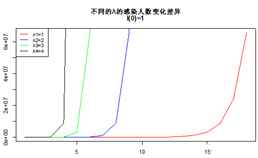
上图不同的颜色曲线代表不同的λ值造成的感染人数变化。

可以看出，λ值越大，传染人数增长的就越快！

假设初只有1个人被感染，即I(0)=1时，不做任何干预和控制的前提下

当λ=4，也就是黑色的曲线到了第3天第4天后，几乎就竖直的往上窜了，变化速度简直就是火箭；

而当λ=1，到了第17天左右，感染人数才开始迅速上升

这2种增长速度的差异是相当惊人的，虽然人数只差了3个人。

当然极端情况下λ=0是的，因为只要从初时刻发现病人迅速隔离，那么就能够直接杜绝传染病的蔓延。

从传染病模型推导出来的不同指数级增长之间的差异如此的巨大，当时我是直接一个震撼：

这就是为什么要大家宅在家里别出去，背后数字上跃迁的可怕！

这也解释了武汉人民做这么大牺牲，通过“封城”来阻断疫情的发展的意义！

这也从定量解读的层面阐述了小区、村落要封闭，虽然在短期内对生活带来不便，但实际上对疫情控制有重要的意义！

但λ=0是这个是理想状态，且不适合于普通的社会环境。因为那是在大家都对这个传染病有了解和认知的情况下。而且某些传染病的症状和普通可自愈（治愈）的疾病症状很相似，也就是人们一开始并没在意，因此就会有后续的传播。

不过对于已经收治的病人，本身传染病病房隔离措施比较好，治疗室里面假设仪器、医护人员、消杀措施配置都到位的情况下，就能实现上面的目的。可医疗资源是有限的，因此当一个区域的医疗资源比较紧张或者用罄后，就必须补充或支援。

这个时候我们就看到了全国各地的医疗队伍驰援武汉的场景，甚至看到了让人心潮澎湃和泪目的各个医疗专家队伍的请战书。

感兴趣的朋友可以接着往下看上面这个简单传染病模型推导的过程

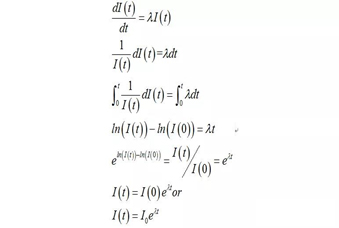
接下来再逐步把模型的应用具体化一些，就是观察某个区域的传染速度。

 

二、SI 模型

这个模型看懂了，你就明白为啥戴口罩，哪怕带自制的口罩不只是对自己负责，也是对这个社会负责。

 我们假设某个观察区域的总人数N不变，不考虑区域内出生和其他原因的死亡，也不考虑人口迁移。

增加需要考虑的是，病人每日接触到的人不全是健康的人，包括已经被感染的人群。这样的话后者是不会再考虑进这个系统；

另外考虑到感染需要一定的条件，因此不是每次病人的接触都会造成感染，存在一个感染的概率

模型的变量稍微调整如下:

t时刻的总人口数保持不变=N，用符号N(t) =N表示，；

t时刻的易感染者（Susceptible）人数，用符号S(t)表示；

t时刻的已感染者（Infective）人数，用符号I(t)表示；

可知，t时刻的N(t)= S(t) + I(t)

β为感染者接触到易感染者后，易感染者被感染的概率；

每个已感染者每天有效接触的人数为λ，但由于接触到的人可能是已经被感染过的了，因此要剔除掉这部分人。

假设t时刻平均易感染人数占比为S(t)/N(t)，那么每天每个已感染者能够让λ[S(t)/N(t)]β个健康者感染，那么每天新增的被感染人数为λ [S(t)/N(t)] β I(t)。

建立模型：

建立模型：

然后以此建立微分方程

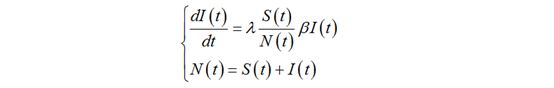
解这个微分方程，和上面的解法相比略有复杂，需要用到“常数变易法”。

首先，将第二个方程变形，S(t) = N(t) – I(t)代入到个方程得到

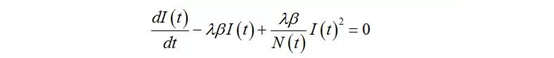
（1.5）的解就是SI模型中受感染人数随时间变化的值，如下

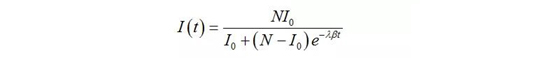
我们看式子(1.6)可以发现，感染率β成为影响传染病传染速度的又一个新增因子，由于它＜1，而且λ和它直接相乘，说明它会直接影响感染人数的增长。

那到底影响有多大呢，数据分析告诉你。

 同样的，我们还是对比一下不同的传染人数和感染率下，被感染人数的变化情况

假设某个时点在一个50万人口的县城，由于普及了公共卫生医疗，条件比较好，某种疾病的感染率β为10%，我们分别比对一下不同的有效接触人数下感染人数增长的速度。

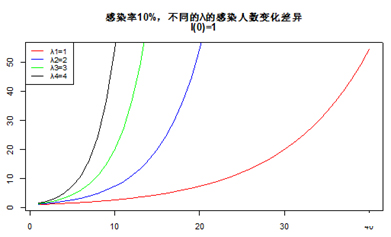
可以看到，由于感染率β值不高，传染病传染的传播速度受到了大幅削弱

当λ=1，到了第40天，受感染人数仅接近55人，占总人口比例很小；

而当λ=4，要到第10天，感染人数也就达到上面这个水平！

这种虽然增长速度很快，但是受感染的力度被β大幅削弱了。

因此，和上面那个例子分析一对比，同样的天数受感染的人数下降的有多快！

 那么假如对比另外一个县城，人口也是50万，假设卫生条件要差，感染率高达30%，我们再来分别比对一下不同的有效接触人数下感染人数增长的速度。

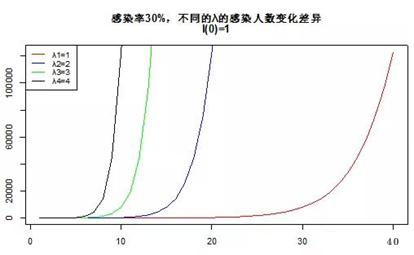
可以看到，由于感染率β值是原来的3倍，传染病传染的传播速度一下子就提升了

当λ=1，到了第40天，受感染人数接近12.3万人，占总人口比例约25%；

而当λ=4，要到第10天，感染人数也达到上面这个水平！

另外，我们还可以看到感染人数的值I(t)，实际上是机器学习里面的Logistics模型的变形，而它是有峰值的。

如下图我们可以看出，假设λ=2，如果大家都讲卫生，做好自己的防护，感染率从30%降到10%的话，感染的峰值出现的时间会从25天延长到90天。

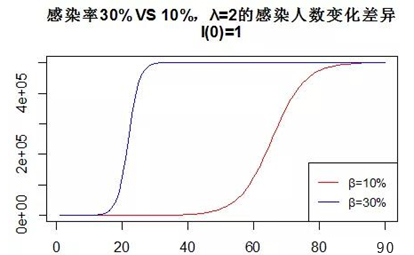
现在我们再仔细想一下，为什么我们要出门戴口罩，不去和人肢体触碰，要勤洗手，就是要大幅的降低病毒的感染成功率，也就是把感染率给降下来！

那我认真去做了，对社会有多少贡献？

从这个计算中我们可以看出，如果戴口罩能将感染率能降3倍，那么传染病造成的感染人数的增速，能够下降上千倍！是55人和12.3万人的区别啊！

并且，如果注意个人防护，戴口罩出门、勤洗手勤消毒，就很可能把疾病传染的速度给压制下去，那是25天出现峰值和3个月后才出现的峰值的区别啊！这段时间差内我们是可以做很多事情和干预措施的。

 这可真是事半功千倍！

 换句话说，不必奢求N95，你哪怕只买到了普通的医用外科口罩，你对防止疾病传播的贡献，超出你的想象！

有兴趣的小伙伴，接下来可以看看上面结论的简单推导过程

可见，变形后的方程左边是一阶线性齐次微分方程，而方程右边≠0，所以先计算左边=0的场景

下面求C，假设C=u(x)，将上面的结论回代得原微分方程形式

我们把a= λβ和b= λβ/N(t) 代入得到上式中，就可以得到

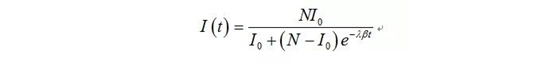
不过，我们接下来再增加一些模型的复杂度，让它再接近些实际。

 

三、SIS和SIR 模型

 这2个模型看懂了，你就更能深刻地理解各地医护人员除了要驰援湖北、武汉外，为啥要用的基建狂魔的特有速度，在各地建设当地的“小汤山”和“方舱”。

 

另外，看懂了模型中的几个参数的组合（其实不难懂），你就明白专家们说的R0＞1和＜1是咋回事儿了？

上面的模型中，我们假设某个观察区域的总人数N不变，不考虑区域内出生和其他原因的死亡，也不考虑人口迁移。考虑了不充分接触的场景，也考虑了感染率的场景，SIS和SIR模型的区别，在于下面2点：

SIS 模型增加需要考虑的是，某些传染病病人是能够被治愈的。不过由于自身没有形成免疫（例如伤风、普通流感），康复的人还会有一定的几率重新被传染；

SIR 模型增加需要考虑的是，病人被治愈后，自身形成了免疫（例麻疹），康复后便终身不再被传染；

因此模型的变量稍微调整如下：

t时刻的总人口数保持不变=N，用符号N(t) =N表示，；

t时刻的易感染者（Susceptible）人数，用符号S(t)表示；

t时刻的已感染者（Infective）人数，用符号I(t)表示；

t时刻的康复者（Recovered）人数，用符号R(t)表示；

可知，对于SIS模型而言，t时刻的N(t)= S(t) + I(t)

      对于SIR模型而言，t时刻的N(t)= S(t) + I(t)+R(t)

β为感染者接触到易感染者后，易感染者被感染的概率；

γ为平均每日被感染者康复人数占总被感染人数的比率；

λ定义如前，为每个已感染者每天有效接触的人数；

 

现在分别讨论SIS和SIR模型

 先讨论SIS模型

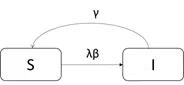
建立模型：

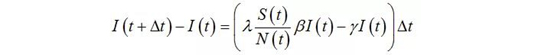
并在此上建立微分方程

如果刚才读了SI模型的推导部分的小伙伴，其实很容易就能依据之前的方法得到（1.8）的解，这个解也就是SIS模型下被感染人数随着时间变化而变化的值

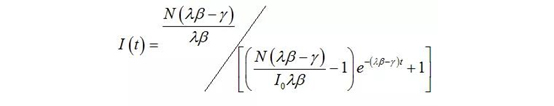
这个看上去很多蝌蚪在游的公式，揭示了什么呢？

  考虑了治愈和康复的情况，治愈率哪怕再低都好（假设只有10%），不考虑愈后自身产生免疫，得到治疗和得不到治疗之间的差异有多大？

我们假设还是那个50万人口的小县城，初感染人数还是1，感染率还是30%，没有封闭的措施，每天已感染者有效接触人数λ=2，我们做一下对比。

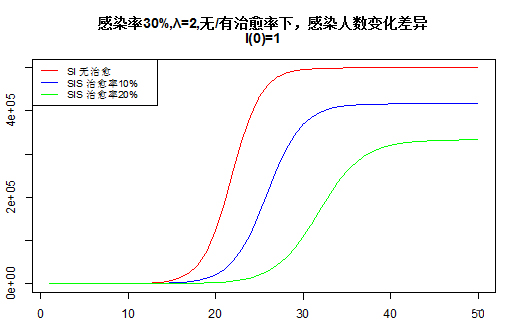
我们看，在前提假设不变的情况下：

如果没有得到治疗，到了25天时感染人数出现峰值；

如果有得到治疗，哪怕只有10%的治愈率，感染人数的峰值出现的时间都晚出现5-6天，不仅如此，感染人数的峰值也相差接近1万人；

如果有得到治疗，哪怕治愈率从10%只是上升到20%，感染人数的峰值出现的时间就能晚出现15天左右，不仅如此，感染人数的峰值也相差接近2万人，减少了约40%！

现在我们可以定量的了解，我们发挥基建狂魔的优势，迅速的在10天内建好“火神山”、“雷神山”，以至于全国各地都在抓紧时间抢建自己的“小汤山”和“方舱”，甚至征用党校和学校、大型馆场做“方舱”的意义有多大！

 每天多治愈一例病人，就意味着全体的传染的人数会有机会大幅的降低。

这就是和时间的赛跑！

 另外，在这个模型里的几个参数，能够构建出我们经常看到文章里专家们说的R₀。

想要理解R₀，就必须从这模型中的几个参数理解开始。

I(t)，代表t时刻被感染者的总数，这个已知；

λ，每个已感染者平均每天接触到的能有效传染的人数。这个容易理解；

β，已感染者平均能够成功传染给易感染者的概率，这个容易理解，感染率嘛；

γ，平均每天被感染者康复人数占总患病人数的比率，这个也容易理解，治愈率嘛；那么1/γ就是平均的传染期（这个需要好好消化一下）。

现在开始讲R₀ （ReproductiveNumber），它代表了一个被感染者在整个传染期内能够进行继发传染的人数。以下图为例，假设 λ= 2

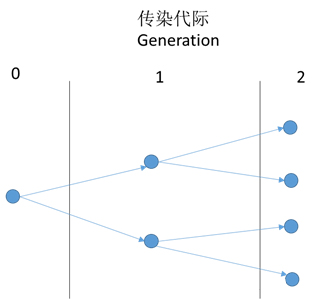
上图就是一个继发传染的代际图，表示了如果λ= 2的时候被感染的速度在第1代时是1传2，在第二代的时候是2传4，如此以往，被感染的病人越来越多。这个时候我们说传染病会爆发。

在不同的模型里面，由于参数的不同，R₀的内涵是略有不同，但可以作为一个阈值来判断在该模型下传染病是否会终爆发或终止。

以SIS模型为例，R₀= λβ/γ。

它的物理意义把公式变形一下就好理解了，R₀= λβ[1/γ]，就是说R₀代表平均每个被感染者在一个传染期内，在感染率的约束下，能够传染有效接触的人的数量。

换句话说这就是一个传染病“杀伤力”指标

从上面的公式中，我们发现：

如果γ越大，也就是治愈率越高，那么一个传染期就会拉长，R0就会越小。

如果λ越小，也就是被感染者接触到健康人的数量越少，那么R0也会越小。这个很自然，你连传染病传播的土壤都给破坏了，它还怎么爆发呢？

如果β越小，也就是感染率越低，那么R0就会越小，这个就不在话下了。

因此，从R0的内涵这一点上也说明了，武汉人民付出巨大牺牲采取的“封城”、全国人民“躺在家里不给添乱”、“出门戴口罩”、“勤洗手”、“10天建成一座‘火神山’”、“驰援武汉、驰援湖北”，等等措施都是有其重要的价值和意义的。

 回到R0本身我们再看：

如果R₀＞1，也就是说1个被感染者如果能够在一个传染期内传染到至少1个人，那么逻辑上就知道整个群体被感染只是时间上的问题；

如果R₀＜1，也就是说1个被感染者连一个人都传染不了了，那么传染病就会终被终止；

不过，R₀的参数中，各个值都是在不断的变化的，因此R0本身也不是个固定的值。但是他可以作为一个阈值来监测，越早发现它比1大，越有利于控制传染病的后续“杀伤力”。

 然后是SIR模型

建立模型

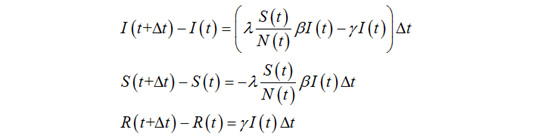
并在此之上建立微分方程

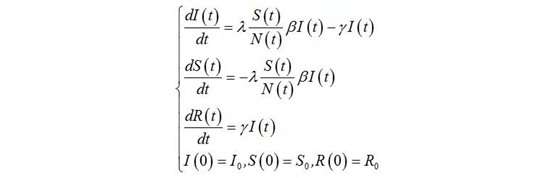
方程(1.11) 是没有解析解的。因此得转到相平面来讨论这个解的性质。

为了能够在二维平面内显示相轨线的变化，我们先通过一个特定的S(0)/N和I(0)/N初始值，根据（1.11）式求出I(t)和S(t)的相轨线方程。

令s(t)=S(t)/N, s₀= S(0)/N和 i(t)=I(t)/N, i₀= I(0)/N

做出相轨迹图如下

上图中的红色箭头是相轨迹中s(t)变化方向。

上图（左）有一个显而易见的认知在生活中是成立的，也就是说当健康人数比率逐渐下降时，说明有传染病发生。当然了，被感染人数比率就自然会上升。

当感染人数比率达到峰值的时候，也就是当健康人数比率达到1/R₀的时候。以上图左为例，1/R₀=0.1，也就是R₀= 10（假设），那已经是一个相当高的恶性传染病了水平了，或者说发生什么严重的事故了。

如果一开始R₀控制的不够好，例如R₀偏大，此时1/R₀出现在s₀左侧足够远，那么必然会有传染病暴发的。像这次NCP来势汹汹，其实主要原因倒不是我们的公共卫生条件多不好，而是错过了黄金时期。到了后来才去大面积的去进行“刮骨疗伤”，去对λ、β、γ这些有关R₀如何降下来的措施下猛药。

而上图（右），一开始1/R₀出现在值，于是迅速的往下滑，这就是因为缺少传播者或者传播的途径非常难，终传染病终止了。而缺少传播者，要么就是提前预警的早，做好了准备（如疫苗、公共卫生宣传和建设），也可以是中途加大了干预（有专门的药物，且很普及）、或遇到了对传播不力的环境因素（如气温升高…..等）；要么就是这种疾病传染力不强。不过这次来看NCP本来可以是服从第二种的轨迹线的，希望这次的教训之后，前事不忘后事之师，我们都能对自己的子孙后辈们负责。

有兴趣的小伙伴，接下来可以看看SIR相轨迹方程的简单推导过程

由（1.11）进行变形

当然了，还有更多的影响感染人数的因子的模型，本次文章没有提到。

例如包含潜伏期的模型、考虑超级传染者的模型、考虑传染模式的模型……，出于篇幅及知识储备所限，本次我就不再引用了。

还是不忘强调下，通过这次简单的学习，我发现定量的去理解一个道理，有时候确实比定性的去理解它要深刻的多。我也就更深刻理解到这次全民抗疫行动的很多措施的意义。

CPDA数据分析更多实战案例：

http://www.chinacpda.com/case/

查找您周边省份授权培训中心：http://www.chinacpda.com/train/