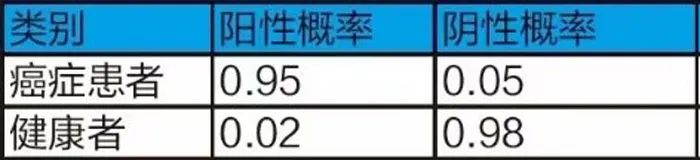
以参加此次体检的100000人的一个群体为例：这里真正患这种癌症的有100（100000*0.1%）人，被报出阳性的人数为100*0.95=95人没有患癌的有99900人，这些人中被报出阳性的有99900*0.02=1998人那一共被爆出阳性的有95+1998=2093人。注意，这里大多数都是假阳性。所以，在这100000人中，如果凭借一个人的报告为阳性来判断他患癌的概率仅为95/(95+1998)=4.54%推理结果是不是跟我们预期的完全不同呢？在这个意义上讲，这位朋友完全不需要如此悲观。