CPDA数据分析在相关系数测量两个变量之间的关联强度，数据分析师常见的相关系数称为 Pearson乘积矩相关系数，用于测量以区间或 比率量表度量的变量之间 的线性关联强度 。

CPDA数据分析师是如何解释相关系数

相关系数的符号和值描述了两个变量之间关系的方向和大小。

数据中的相关系数值在-1和1之间。

相关系数的值越大，线性关系越强。

强的线性关系由-1或1的相关系数表示。

弱的线性关系由等于0的相关系数表示。

正相关表示如果一个变量变大，则另一个变量趋于变大。

负相关表示如果一个变量变大，则另一个变量趋于变小。

请记住，皮尔逊积矩相关系数仅测量线性关系。因此，相关性为0并不意味着两个变量之间的关系为零。相反，它意味着零线性关系。（两个变量可能同时具有零线性关系和强曲线关系。）

有关散点图和相关系数的解释

为了CPDA学员可以很好的对散点图相关系数更快的理解，我们采用举例的方法来为大家讲解有关数据分析散点图系数的介绍，散点图显示了不同的数据模式如何产生不同程度的相关性。

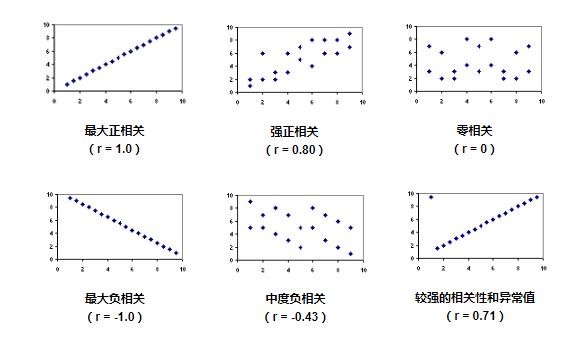
我们从散点图可以明显看出几点。

当图中直线的 斜率为负时，相关为负；反之，则为负。反之亦然。

当数据点恰好位于一条直线上时，会出现强的相关性（r = 1.0和r = -1.0）。

随着数据点变得更加分散，相关性变得更弱。

如果数据点属于随机模式，则相关性等于零。

相关性受异常值影响 。比较个散点图和一个散点图。一个图中的单个异常值极大地降低了相关性（从1.00降低到0.71）。

下面CPDA数据分析师给出了计算乘积矩相关系数（r）的常用公式。

乘积矩相关系数。 两个变量之间的相关性r为：

r =Σ（xy）/ sqrt [（Σx 2）*（Σy 2）]

其中Σ是求和符号，x = x i - x，x i是观察i的x值， x是平均值x值，y = y i - y，y i是观察i的y值， y是平均值y值。

下面的公式使用总体平均值和总体标准差从总体数据中计算总体相关系数（ρ）。

人口相关系数， 两个变量之间的相关性ρ为：

ρ= [1 / N] *Σ{[（X 我 - μ X）/σ X ]

* [（Y 我 - μ Ý）/σ ÿ ]}

其中，N是在人口观测值的数量，Σ是求和符号，X 我是用于观察i中的X值，μ X是总体平均值为变量X，Y 我是用于观察在Y值i，μ ÿ被总体平均值为变量Y，σ X是X的总体标准偏差，σ ÿ是Y的总体标准偏差

以下公式使用样本均值和样本标准差从样本数据计算样本相关系数（r）。

样本相关系数。 两个变量之间的相关性r为：

r = [1 /（n-1）] *Σ{[（（x i - x）/ s x ]

* [（y i - y）/ s y ]}

其中n是样本中的观察次数，Σ是求和符号，x i是观察i的x值， x是x的样本均值，y i是观察i的y值， y是样本均值在y中，s x是x的样本标准偏差，而s y是y的样本标准偏差。

样本相关系数的解释取决于样本数据的收集方式，对于大的 简单随机样本，样本相关系数是总体相关系数的无偏估计。

后两个公式均可从个公式导出。当数据分析师拥有整个总体的数据时，请使用个或第二个公式。当数据分析师仅具有样本数据但要估计总体中的相关性时，请使用第三个公式。如有疑问，请使用个公式。

CPDA数据分析师几乎不需要手工计算相关系数。许多软件包（例如Excel）和大多数 图形计算器 都具有关联功能，可以为您完成这项工作。