Excel提供了解决该示例问题所需的所有任务

 CPDA数据分析师举例来为我们讲解根据（1）智商和（2）学生学习的小时数，开发出小二乘回归方程来预测考试成绩来作一个案例演示，让学员可以更佳深入的明白，评估回归方程预测测验分数（因变量）的程度，CPDA会评估每个独立的变量（即智商和学习时间）对预测的贡献。

让我们来看下Excel产生哪些输出，看看它如何解决每个任务。

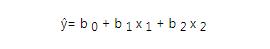
再这个等式中，ŷ是预测的考试的成绩。自变量是IQ和学习时间，分别由x 1和x 2表示。回归系数为b 0，b 1和b 2。在等式的右边，的未知数是回归系数。因此，要指定方程式，我们需要为系数分配值。

 再我们讲矩阵的时候，展示了如何使用矩阵代数-手工耗时，费力的过程将值分配给回归系数。Excel在幕后进行所有艰苦的工作，并将结果显示在回归系数表中：

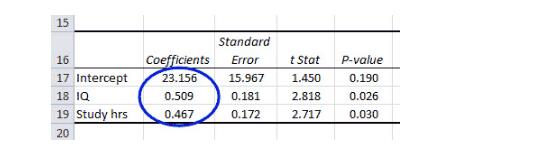
在这张表里面我们看到回归截距（b 0）为23.156，智商的回归系数（b 1）为0.509，学习时间的回归系数（b 2）为0.467。因此，小二乘回归方程可以重写为：

ŷ= 23.156 + 0.505 *智商+ 0.467 *小时

这是满足小二乘标准的线性方程。这意味着该方程比其他线性方程更好地拟合了根据其创建的数据。

多重确定系数

我们的方程式比其他线性方程式更适合数据的事实并不能保证它很好地适合数据。我们仍然需要问：我们的方程式对数据的拟合程度如何？

 为了回答这个问题，研究人员着眼于多重确定系数（R 2）。多重确定系数衡量因变量的变化比例，可以从回归方程中的一组自变量中预测出因变量的变化比例。当回归方程很好地拟合数据时，R 2将会很大（即接近1）；反之，R 2将会很大。反之亦然。

 可以通过平方和来定义倍数确定系数：

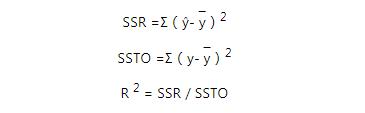
其中SSR是归因于回归的平方和，SSTO是平方和的总和，ŷ是因变量的预测值，y是因变量平均值，y是因变量原始得分。

回归系数的意义

通过多元回归，可以有多个自变量。因此，很自然地要问，在考虑了其他变量的影响后，特定的自变量是否对回归有显着贡献。这个问题的答案可以在回归系数表中找到：

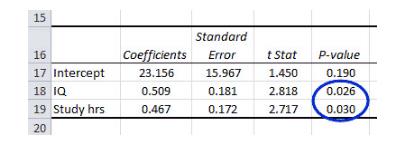
回归系数表显示了每个系数的以下信息：其值，其标准误差，t统计量和t统计量的显着性。在此示例中，智商和学习时间的t统计量均在0.05水平上具有统计学意义。这意味着在考虑学习时间的影响后，智商对回归的贡献很大。在考虑了智商的影响后，学习时间对回归的贡献很大。

单的三个步骤教你在Excel中进行数据输入：

http://www.chinacpda.com/qa/detail/?id=666

简用Excel进行回归分析让你的团队可以根据数据做出更好的决策：

http://www.chinacpda.com/qa/detail/?id=665

CPDA数据分析师在线学习班正式启动:

http://www.chinacpda.com/data/detail/?id=623

查找您周边省份授权培训中心：

http://www.chinacpda.com/train/

2020年CPDA数据分析师线上报名：

http://www.chinacpda.com/baoming.php

免费客服热线：400-050-6600

商业联合会数据分析专业委员会